Question

【题目】如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S△ABF=S△ADF②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是（　　）

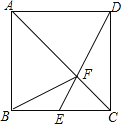
A. ①③ B. ②③ C. ①④ D. ②④

Answer 1

【答案】C

【解析】分析：由△AFD≌△AFB，即可推出S△ABF=S△ADF，故①正确，由BE=EC=BC=AD，AD∥EC，推出 =，可得S△CDF=2S△CEF，S△ADF=4S△CEF，S△ADF=2S△CDF，故②③错误④正确，由此即可判断．

详解：∵四边形ABCD是正方形，
∴AD∥CB，AD=BC=AB，∠FAD=∠FAB，
在△AFD和△AFB中，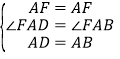

∴△AFD≌△AFB，
∴S△ABF=S△ADF，故①正确，
∵BE=EC=BC=AD，AD∥EC，
∴=，
∴S△CDF=2S△CEF，S△ADF=4S△CEF，S△ADF=2S△CDF，
故②③错误④正确，
故选：C．