Question

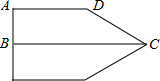如图，直角梯形ABCD中，AD∥BC，A=90°，将两个这样的全等直角梯形的一条底边重合，恰好拼成一个各边长都相等的五边形，若这个五边形的面积为12+3

3

，则原直角梯形的底边BC长是

3+2

3

．

Answer 1

分析：首先过点D作DK⊥BC于K，易证得四边形ABKD是矩形，根据题意即可得：AD=CD=EC=EF=AF=2AB，求得∠DCK=30°，然后根据梯形的面积公式，列方程求解即可求得答案．

解答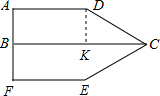：解：过点D作DK⊥BC于K，
∵直角梯形ABCD中，AD∥BC，∠A=90°，
∴∠A=∠ABK=∠DKB=90°，
∴四边形ABKD是矩形，
∴BK=AD，DK=AB，
根据题意得：AD=CD=EC=EF=AF=2AB，
∴CD=2DK，
∴∠DCK=30°，
∴KC=

3

DK=

3

AB，
设AB=x，
则S_梯形ABCD=

1

2

S_{五边形AFECD}=

12+3 3

2

，S_梯形ABCD=

1

2

（AD+BC）•AB=

1

2

（2x+2x+

3

x）•x，
∴

1

2

（x+x+

3

x）•x=

12+3 3

2

，
解得：x=

3

，
∴BC=2x+

3

x=3+2

3

．
故答案为：3+2

3

．

点评：此题考查了直角梯形的性质，直角三角形的性质．此题难度适中，解题的关键是注意数形结合思想与方程思想的应用，注意辅助线的作法．