题目内容
若0<n<m,m2+n2=10,nm=3,求m2-n2的值.
考点:完全平方公式,平方差公式
专题:计算题
分析:利用完全平方公式列出关系式,把已知等式代入求出m+n与m-n的值,原式利用平方差公式化简,将各自的追代入计算即可求出值.
解答:解:∵0<n<m,m2+n2=10,nm=3,
∴(m+n)2=m2+n2+2mn=10+6=16,即m+n=4;(m-n)2=m2+n2-2mn=10-6=4,即m-n=2,
则原式=(m+n)(m-n)=8.
∴(m+n)2=m2+n2+2mn=10+6=16,即m+n=4;(m-n)2=m2+n2-2mn=10-6=4,即m-n=2,
则原式=(m+n)(m-n)=8.
点评:此题考查了完全平方公式,以及平方差公式,熟练掌握公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列四组线段中,可以构成直角三角形的是( )
A、1,
| ||||||
B、3
| ||||||
| C、7,15,17 | ||||||
| D、2,4,6 |
下列各组代数式没有公因式的是( )
| A、5a-5b和5a+5b |
| B、ax+y和x+ay |
| C、a2+2ab+b2和2a+2b |
| D、a2-ab和a2-b2 |
在实数
,0,-
,
,π,3.14,无理数的个数有( )
| 22 |
| 7 |
| 9 |
| 3 | 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
在5,2006,0,-2
,-
中,负数有( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
在-
、2π、
、
、0、
中无理数个数为( )
| (-5)2 |
| 36 |
| 1 |
| 7 |
| 3 | 11 |
| A、1个 | B、2个 | C、3个 | D、4个 |
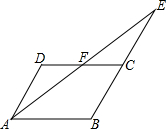 如图,四边形ABCD是平行四边形.点E在BC的延长线上,且CE=BC,连接AE交DC于点F.
如图,四边形ABCD是平行四边形.点E在BC的延长线上,且CE=BC,连接AE交DC于点F.