题目内容
13．
如图，一个高16m，底面周长8m的圆柱形水塔，现制造一个螺旋形登梯，为了减小坡度，要求登梯绕塔环绕一周半到达顶端，问登梯至少多长？
分析 要求登梯的长，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果，在求线段长时，借助于勾股定理．
解答 解：将圆柱表面切开展开呈长方形，
∵圆柱高16m，底面周长8m，
∴x2=（1×8+4）2+162=400，
∴登梯至少$\sqrt{400}$=20（米）．
点评 本题考查了勾股定理的应用．圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，高等于圆柱的高，本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
3．
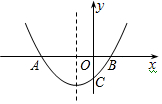如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，∠OBC=45°，则下列各式成立的是（ ）
如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，∠OBC=45°，则下列各式成立的是（ ）| A． | 1-b+c=0 | B． | 1+b+c=0 | C． | 1+b-c=0 | D． | 1-b-c=0 |
1．大于-2.5，不小于2的整数共有（ ）个．
| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
如图，∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，从左起第1个等边三角形的边长记为a1，第2个等边三角形的边长记为a2，以此类推．若OA1=1，则a2016=22015．
2．5.24万精确到（ ）
| A． | 十分位 | B． | 百分位 | C． | 万位 | D． | 百位 |