题目内容
在Rt△ABC中,∠BCA=90°,CD是中线,AC=6,CD=5,求sin∠ACD、cos∠ACD和tan∠ACD.
解:∵∠BCA=90°,CD是中线,
∴CD= AB=AD=BD,
AB=AD=BD,
∴∠A=∠ACD,AB=2CD=10,
在Rt△ABC中,
∴BC= =8,
=8,
则sin∠ACD=sin∠A= =
= ,
,
cos∠ACD=cos∠A=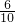 =
= ,
,
tan∠ACD=tan∠A= =
= .
.
分析:如图,利用在直角三角形中斜边上的中线等于斜边的一半求得AB的值后,根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后再代入三角函数进行求解.
点评:解题的关键是利用在直角三角形中斜边上的中线等于斜边的一半求得AB的值,本题考查解直角三角形的定义,由直角三角形已知元素求未知元素,只要理解直角三角形中边角之间的关系即可求解.
∴CD=
 AB=AD=BD,
AB=AD=BD,∴∠A=∠ACD,AB=2CD=10,

在Rt△ABC中,
∴BC=
 =8,
=8,则sin∠ACD=sin∠A=
 =
= ,
,cos∠ACD=cos∠A=
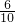 =
= ,
,tan∠ACD=tan∠A=
 =
= .
.分析:如图,利用在直角三角形中斜边上的中线等于斜边的一半求得AB的值后,根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后再代入三角函数进行求解.
点评:解题的关键是利用在直角三角形中斜边上的中线等于斜边的一半求得AB的值,本题考查解直角三角形的定义,由直角三角形已知元素求未知元素,只要理解直角三角形中边角之间的关系即可求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )