题目内容
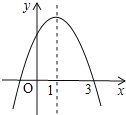
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论①abc>0②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3③4a+2b+c<0④当x>0时,y随x的增大而减小正确的是( ).
A.①③④B.②④C.①②③D.②
【答案】D
【解析】
由函数图象可得抛物线开口向下,得到a<0,又对称轴在y轴右侧,可得b>0,根据抛物线与y轴的交点在y轴正半轴,得到c>0,进而得到abc<0,结论①错误;由抛物线与x轴的交点为(3,0)及对称轴为x=1,利用对称性得到抛物线与x轴另一个交点为(-1,0),进而得到方程ax2+bx+c=0的两根分别为-1和3,结论②正确;由图像可知,当x=2时,y>0,即4a+2b+c>0,结论③错误;由抛物线的对称轴为直线x=1,得到对称轴右边y随x的增大而减小,对称轴左边y随x的增大而增大,故x大于0小于1时,y随x的增大而增大,结论④错误.
解:∵抛物线开口向下,∴a<0,
∵对称轴在y轴右侧,∴![]() >0,∴b>0,
>0,∴b>0,
∵抛物线与y轴的交点在y轴正半轴,∴c>0,
∴abc<0,故①错误;
∵抛物线与x轴的一个交点为(3,0),又对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(-1,0),
∴方程ax2+bx+c=0的两根是x1=-1,x2=3,故②正确;
∵x=2时, y>0,
∴4a+2b+c>0,故③错误;
∵由函数图象可得:当0<x<1时,y随x的增大而增大;
当x>1时,y随x的增大而减小,故④错误;
故选:D.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
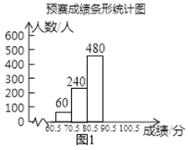
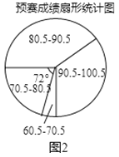
初中学业考试导与练系列答案【题目】为了弘扬中华优秀传统文化,用好汉字,某中学开展了一次“古诗词”知识竞赛,赛程共分“预赛、复赛和决赛”三个阶段,预赛由各班举行,全员参加,按统一标准评分,统计成绩后绘制成如图1和图2所示的两幅不完整“预赛成绩条形统计图”和“预赛成绩扇形统计图”,预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”(采用百分制记分,得分都为60分以上的整数).
前10名选手成绩统计表
序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
预赛成绩(分) | 100 | 92 | 95 | 98 | 94 | 100 | 93 | 96 | 95 | 96 |
复赛成绩(分) | 90 | 80 | 85 | 90 | 80 | 88 | 85 | 90 | 86 | 89 |
总成绩(分) | 94 | 84.8 | 89 |
| 85.6 | 92.8 | 88.2 |
| 89.6 | 91.8 |
(1)求该中学学生的总人数,并将图1补充完整;
(2)在图2中,求“90.5~100.5分数段人数”的圆心角度数;
(3)预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”,若按预赛成绩占40%,复赛成绩占60%的比例计算总成绩,并从中选出3人参加决赛,你认为选哪几号选手去参加决赛,并说明理由.