题目内容
.平行四边形ABCD中,AB:BC=3:2,∠DAB=6 0°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于 .
0°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于 .

2 :
:
【解析】
解:连接DE,DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
根据题意得, ,
,
∴AF·DP=CE·DQ.
设AB=3a,则AE=BF=a,EB=BC=2a.
易得∠CBM=∠DAE=60°,
∴∠BFN=∠BCM=30°,
∴在Rt△BFN和Rt△BCM中,
BN=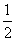 BF=
BF=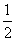 a,BM=
a,BM=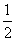 BC=a,CM=
BC=a,CM= a,
a,
∴AN=3.5a,EM=3a,
在Rt△ANF和Rt△ECM中应用勾股定理得,
AF= a,CE=
a,CE= a,
a,
∴
∴

【难度】较难

练习册系列答案
相关题目
 四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.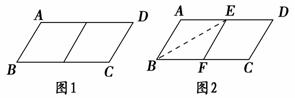


 沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为 .
沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为 . .
. 的图象交于A,B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B,O,E,P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .
的图象交于A,B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B,O,E,P为顶点的四边形是平行四边形,则满足条件的P点坐标是 . 的对角线
的对角线 ,
, ,则图中五个小矩形的周长之和为_______.
,则图中五个小矩形的周长之和为_______.
