题目内容
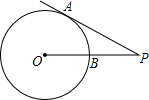
如图，PA切⊙O于A，AB⊥OP于B，若PO=8 cm，BO=2 cm，则PA的长为
- A.16cm
- B.48cm
- C.6
cm - D.4cm
D
分析：根据题意，易证△PAB∽△POA，运用相似形的性质求解．
解答：PA切⊙O于A，则OA⊥PA，
又∵AB⊥OP于B，则△PAB∽△POA，
因而
，
根据PO=8 cm，BO=2 cm，则PB=6cm，
得到
，
解得PA=4．
点评：主要考查了相似三角形的判定和性质定理．
分析：根据题意，易证△PAB∽△POA，运用相似形的性质求解．
解答：PA切⊙O于A，则OA⊥PA，
又∵AB⊥OP于B，则△PAB∽△POA，
因而
，根据PO=8 cm，BO=2 cm，则PB=6cm，
得到
，解得PA=4
．点评：主要考查了相似三角形的判定和性质定理．
练习册系列答案
相关题目
如图，PA切⊙O于点A，PO交⊙O于点B，若PA=6，BP=4，则⊙O的半径为（ ）A、
| ||
B、
| ||
| C、2 | ||
| D、5 |
如图，PA切⊙O于点A，PBC是⊙O的割线，且PB=BC，如果PA=3| 2 |
A、3
| ||
| B、3 | ||
C、
| ||
D、2
|
8、如图，PA切⊙O于点A，PBC是⊙O的割线且过圆心，PA=4，PB=2，则⊙O的半径等于（ ）
如图，PA切⊙O于点A，PB切⊙O于点B，如果∠APB=60°，⊙O半径是3，则劣弧AB的长为（ ）A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
如图：PA切⊙O于A，PB切⊙O于B，OP交⊙O于C，下列结论中错误的是（ ）