题目内容
如图,已知抛物线y=
(x-1)(x-b)(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.

(1)点B的坐标为
(2)若b=8,请你在抛物线上找点P,使得△PAC是直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你探索,在(1)的结论下,在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
| 1 |
| 4 |

(1)点B的坐标为
(b,0)
(b,0)
,点C的坐标为(0,
b)
| 1 |
| 4 |
(0,
b)
(用含b的代数式表示);| 1 |
| 4 |
(2)若b=8,请你在抛物线上找点P,使得△PAC是直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你探索,在(1)的结论下,在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
分析:(1)令y=0,解关于x的一元二次方程即可得到点B的坐标,再令x=0求出y的值得到点C的坐标;
(2)先根据b的值确定出点A的坐标,然后写出直线AC的解析式,再分∠CAP=90°和∠ACP=90°两种情况写出直线PC、PA的解析式,与抛物线解析式联立求解即可得到点P的坐标;
(3)根据O、A、B在同一直线上判定三个相似三角形都是直角三角形,所以点QA⊥x轴,然后分∠OCQ=90°和∠OQC=90°两种情况,利用相似三角形对应边成比例列式求出AQ的值,即可得到点Q的坐标.
(2)先根据b的值确定出点A的坐标,然后写出直线AC的解析式,再分∠CAP=90°和∠ACP=90°两种情况写出直线PC、PA的解析式,与抛物线解析式联立求解即可得到点P的坐标;
(3)根据O、A、B在同一直线上判定三个相似三角形都是直角三角形,所以点QA⊥x轴,然后分∠OCQ=90°和∠OQC=90°两种情况,利用相似三角形对应边成比例列式求出AQ的值,即可得到点Q的坐标.
解答:解:(1)令y=0,则
(x-1)(x-b)=0,
解得x1=1,x2=b,
∵b>2,
∴点B的坐标为(b,0),
令x=0,则y=
b,
∴点C的坐标为(0,
b);
(2)b=8时,点A(1,0),C(0,2),
所以,直线AC的解析式为y=-2x+2,
△PAC是直角三角形,分两种情况讨论:
①当∠CAP=90°时,设直线PA的解析式为y=
x+b,
则
×1+b=0,
解得b=-
,
所以,y=
x-
,
联立
,
解得
,
(为点A坐标,舍去),
∴点P(10,4.5);
②当∠ACP=90°时,设直线PC的解析式为y=
x+b,
则
×0+b=2,
解得b=2,
所以,y=
x+2,
联立
,
解得
,
(为点C坐标,舍去),
∴点P(11,7.5);
综上所述,存在P(10,4.5)或(11,7.5)使得△PAC是直角三角形;
(3)∵点O、A、B都在x轴上,
∴要使△QCO、△QOA和△QAB中的任意两个三角形均相似,三个三角形都是直角三角形,
∴点QA⊥x轴,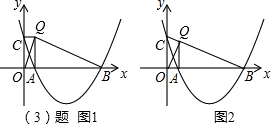
①当∠OCQ=90°时,四边形OAQC是矩形,
∴QA=OC=
b,
∵△QOA∽△BQA∽△OQC,
∴
=
,
∴QA2=AB•OA,
∴(
b)2=(b-1)•1,
整理得,b2-16b+16=0,
解得b=8+4
,b=8-4
(舍去),
∴QA=
b=
×(8+4
)=2+
,
∴点Q的坐标为(1,2+
),
②当∠OQC=90°时,
∵△QOA∽△BQA∽△OCQ,
∴
=
,△OQA∽△OBQ,
∴OQ2=QA•OC,
=
,
∴OQ2=OA•OB,
∴QA•OC=OA•OB,
∴QA•
b=1•b,
解得QA=4,
∴点Q的坐标为(1,4),
综上所述,点Q的坐标为(1,2+
)或(1,4).
故答案为:B(b,0),C(0,
b).
| 1 |
| 4 |
解得x1=1,x2=b,
∵b>2,
∴点B的坐标为(b,0),
令x=0,则y=
| 1 |
| 4 |
∴点C的坐标为(0,
| 1 |
| 4 |
(2)b=8时,点A(1,0),C(0,2),
所以,直线AC的解析式为y=-2x+2,
△PAC是直角三角形,分两种情况讨论:
①当∠CAP=90°时,设直线PA的解析式为y=
| 1 |
| 2 |
则
| 1 |
| 2 |
解得b=-
| 1 |
| 2 |
所以,y=
| 1 |
| 2 |
| 1 |
| 2 |
联立
|
解得
|
|
∴点P(10,4.5);
②当∠ACP=90°时,设直线PC的解析式为y=
| 1 |
| 2 |
则
| 1 |
| 2 |
解得b=2,
所以,y=
| 1 |
| 2 |
联立
|
解得
|
|
∴点P(11,7.5);
综上所述,存在P(10,4.5)或(11,7.5)使得△PAC是直角三角形;
(3)∵点O、A、B都在x轴上,
∴要使△QCO、△QOA和△QAB中的任意两个三角形均相似,三个三角形都是直角三角形,
∴点QA⊥x轴,

①当∠OCQ=90°时,四边形OAQC是矩形,
∴QA=OC=
| 1 |
| 4 |
∵△QOA∽△BQA∽△OQC,
∴
| QA |
| AB |
| OA |
| QA |
∴QA2=AB•OA,
∴(
| 1 |
| 4 |
整理得,b2-16b+16=0,
解得b=8+4
| 3 |
| 3 |
∴QA=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 3 |
∴点Q的坐标为(1,2+
| 3 |
②当∠OQC=90°时,
∵△QOA∽△BQA∽△OCQ,
∴
| OC |
| OQ |
| OQ |
| QA |
∴OQ2=QA•OC,
| OQ |
| OB |
| OA |
| OQ |
∴OQ2=OA•OB,
∴QA•OC=OA•OB,
∴QA•
| 1 |
| 4 |
解得QA=4,
∴点Q的坐标为(1,4),
综上所述,点Q的坐标为(1,2+
| 3 |
故答案为:B(b,0),C(0,
| 1 |
| 4 |
点评:本题是二次函数综合题型,主要考查了求抛物线与坐标轴的交点坐标,联立两函数解析式求交点坐标,待定系数法求一次函数解析式,相似三角形对应边成比例的性质,难点在于(2)(3)两小题都要分情况讨论.

练习册系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;