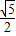题目内容
(2006•扬州)图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=3.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束.(1)试说明在运动过程中,原点O始终在⊙G上;
(2)设点C的坐标为(x,y),试探求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在整个运动过程中,点C运动的路程是多少?

【答案】分析:(1)因为OG始终是⊙G的半径,所以原点O始终在⊙G上;
(2)运动过程中,弧AC的长保持不变,弧AC所对应的圆周角∠AOC保持不变,等于∠XOC,∠xOC=30°,y= .即自变量x的取值范围是
.即自变量x的取值范围是 ≤x≤3
≤x≤3 ;
;
(3)利用勾股定理可求得,点C运动的路程总路径为:C1C2+C2C3=3+6-3 =9-3
=9-3 .
.
解答: 解:(1)∵AB是⊙G的直径,
解:(1)∵AB是⊙G的直径,
∴∠AOB=90°(直径所对的圆周角是直角),
∴原点O始终在⊙G上;
(2)运动过程中,弧AC的长保持不变,
弧AC所对应的圆周角∠AOC保持不变,
由图2可知,∠AOC=30°,y= ,
,
即自变量x的取值范围是 ≤x≤3
≤x≤3 ;
;
(3)解:如图1,连接OG.
∵∠AOB是直角,G为AB中点,
∴GO= AB=半径,
AB=半径,
∴原点O始终在⊙G上.
∵∠ACB=90°,AB=6,AC=3,
∴BC=3 ,
,
连接OC.则∠AOC=∠ABC,
∴tan∠AOC= =
= ,
,
∴点C在与x轴夹角为∠AOC的射线上运动.
如图2,C1C2=OC2-OC1=6-3=3;
如图3,C2C3=OC2-OC3=6-3 ;
;
∴总路径为:C1C2+C2C3=3+6-3 =9-3
=9-3 .
.
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.
(2)运动过程中,弧AC的长保持不变,弧AC所对应的圆周角∠AOC保持不变,等于∠XOC,∠xOC=30°,y=
 .即自变量x的取值范围是
.即自变量x的取值范围是 ≤x≤3
≤x≤3 ;
;(3)利用勾股定理可求得,点C运动的路程总路径为:C1C2+C2C3=3+6-3
 =9-3
=9-3 .
.解答:
 解:(1)∵AB是⊙G的直径,
解:(1)∵AB是⊙G的直径,∴∠AOB=90°(直径所对的圆周角是直角),
∴原点O始终在⊙G上;
(2)运动过程中,弧AC的长保持不变,
弧AC所对应的圆周角∠AOC保持不变,
由图2可知,∠AOC=30°,y=
 ,
,即自变量x的取值范围是
 ≤x≤3
≤x≤3 ;
;(3)解:如图1,连接OG.
∵∠AOB是直角,G为AB中点,
∴GO=
 AB=半径,
AB=半径,∴原点O始终在⊙G上.
∵∠ACB=90°,AB=6,AC=3,
∴BC=3
 ,
,连接OC.则∠AOC=∠ABC,
∴tan∠AOC=
 =
= ,
,∴点C在与x轴夹角为∠AOC的射线上运动.
如图2,C1C2=OC2-OC1=6-3=3;
如图3,C2C3=OC2-OC3=6-3
 ;
;∴总路径为:C1C2+C2C3=3+6-3
 =9-3
=9-3 .
.
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目