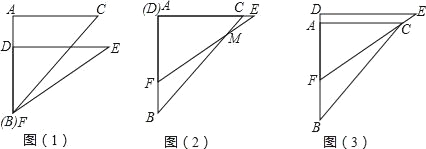
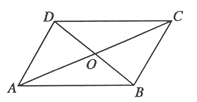
��Ŀ����
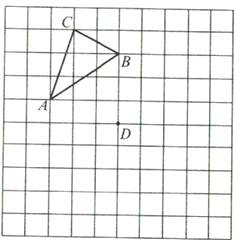
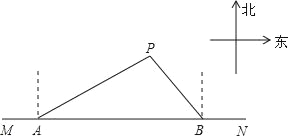
����Ŀ����ͼ���ڶ�������ĺ�����MN����A��B���Ҵ������յ��Ѵ�����dz�Ĵ�P������źţ���֪��P�ڴ�A�ı�ƫ��58������P�ڴ�B�ı�ƫ��35������AP�ľ���Ϊ30����ο����ݣ�sin32���0.53��sin55���0.82����
��1����P��������MN�ľ��루��ȷ��0.1�����
��2������A����B�ֱ���20����/Сʱ��15����/Сʱ���ٶ�ͬʱ����������ֱ��ǰ����Ԯ����ͨ�������ж����Ҵ��ȵ��ﴬP����
���𰸡���1����P��������MN�ľ���ԼΪ15.9�����2��B���ȵ�����
���������⣺��1����ͼ������P��PH��MN�ڵ�H,
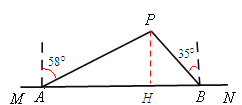
����P�ڴ�A�ı�ƫ��58���������PAH=320��
��AP=30���
��![]() �������
�������
�𣺴�P��������MN�ľ���Ϊ15.9���
��2������P�ڴ�B�ı�ƫ��35���������PBH=550��
��![]() �������
�������
����A����B���ٶȷֱ�Ϊ20����/Сʱ��15����/Сʱ��
����A���ﴬP��ʱ��Ϊ![]() ��Сʱ������B���ﴬP��ʱ��Ϊ
��Сʱ������B���ﴬP��ʱ��Ϊ![]() ��Сʱ����
��Сʱ����
��![]() ������B�ȵ��ﴬP��
������B�ȵ��ﴬP��
��1������P��PH��MN�ڵ�H,����ֱ��������PAH��Ӧ�����Һ���������ô�P��������MN�ľ���PH��
��2�ֱ��������A���ﴬP��ʱ����бȽϼ��ɵó����ۡ�

 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
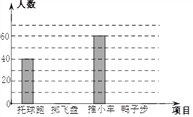
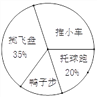
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�����Ŀ��ijУ��3000��ѧ����Ϊ�˽�ȫУѧ������ѧ��ʽ����У��ѧ��ȤС�����ʾ��������ʽ����������˸�У����ѧ������Ҫ��ѧ��ʽ(�����ʾ������ѧ��ֻ�ܴ���������������ѡ��һ��)���������������Ƴ����²�������ͳ��ͼ��
���� | A | B | C | D | E | F |
��ѧ��ʽ | �綯�� | ˽�ҳ� | ������ͨ | ���г� | ���� | ���� |
ijУ����ѧ����Ҫ��ѧ��ʽ����ͳ��ͼijУ����ѧ����Ҫ��ѧ��ʽ����ͳ��ͼ
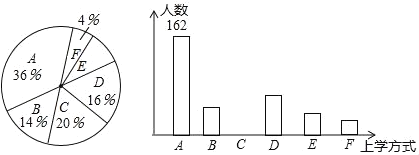
����������Ϣ���ش��������⣺
(1)���뱾���ʾ������ѧ������____�ˣ�����ѡ��B���������____�ˣ�
(2)������ͳ��ͼ�У���E���Ӧ������Բ�Ľ����Ķ���������ȫ����ͳ��ͼ��
(3)����A��C��D��E��������ѧ��ʽ��Ϊ����ɫ������������Ƹ�Уÿ������ɫ��������ѧ��������