��Ŀ����
����Ŀ����֪������y=a��x+3����x��1����a��0������x��������������ཻ��A��B���㣬��y���ཻ�ڵ�C��������A��ֱ��y=�� ![]() x+b�������ߵ���һ������ΪD��
x+b�������ߵ���һ������ΪD��
��1������D�ĺ�����Ϊ2���������ߵĺ�������ʽ��
��2�����ڵ��������ڵ����������е�P��ʹ����A��B��PΪ��������������ABC���ƣ����P�����ꣻ
��3���ڣ�1���������£����E���߶�AD�ϵ�һ�㣨�����˵㣩������BE��һ����Q�ӵ�B���������߶�BE��ÿ��1����λ���ٶ��˶�����E�������߶�ED��ÿ�� ![]() ����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
���𰸡�
��1��
�⣺��y=a��x+3����x��1����
���A����������3��0������B����������1��0����
��ֱ��y=�� ![]() x+b������A��
x+b������A��
��b=��3 ![]() ��
��
��y=�� ![]() x��3
x��3 ![]() ��
��
��x=2ʱ��y=��5 ![]() ��
��
���D��������2����5 ![]() ����
����
�ߵ�D���������ϣ�
��a��2+3����2��1��=��5 ![]() ��
��
��ã�a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() ��x+3����x��1��=��
��x+3����x��1��=�� ![]() x2��2
x2��2 ![]() x+3
x+3 ![]()
��2��
�⣺��ͼ1�У���PH��x����H����� P���꣨m��n����
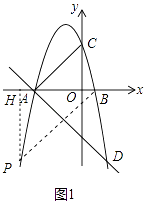
����BPA�ס�ABCʱ����BAC=��PBA��
��tan��BAC=tan��PBA���� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ����n=��a��m��1����
����n=��a��m��1����
�� ![]() ���m=��4��1����������
���m=��4��1����������
��m=��4ʱ��n=5a��
�ߡ�BPA�ס�ABC��
�� ![]() =
= ![]() ��
��
��AB2=ACPB��
��42= ![]() ��
��
���a=�� ![]() ��
�� ![]() ����������
����������
��n=5a=�� ![]() ��
��
���P���꣨��4���� ![]() ����
����
����PBA�ס�ABCʱ����CBA=��PBA��
��tan��CBA=tan��PBA���� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��n=��3a��m��1����
�� ![]() ��
��
���m=��6��1����������
��m=��6ʱ��n=21a��
�ߡ�PBA�ס�ABC��
�� ![]() =
= ![]() ����AB2=BCPB��
����AB2=BCPB��
��42= ![]()
![]() ��
��
���a=�� ![]() ��
�� ![]() ������������������
������������������
���P���꣨��6����3 ![]() ����
����
�������������������ĵ�P�����꣨��4���� ![]() ���ͣ���6����3
���ͣ���6����3 ![]() ����
����
��3��
�⣺��ͼ2�У���DM��x�ύ��������M����DN��x����N����EF��DM��F��
��tan��DAN= ![]() =
= ![]() =
= ![]() ��
��
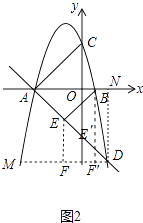
���DAN=60�㣬
���EDF=60�㣬
��DE= ![]() =
= ![]() EF��
EF��
��Q���˶�ʱ��t= ![]() +
+ ![]() =BE+EF��
=BE+EF��
�൱BE��EF����ʱ��t��С��
��BE��DM����ʱ��E���꣨1����4 ![]() ��
��
����������1�����ݶ��κ����Ľ���ʽȷ����A��B�����꣬�������ֱ��AD�Ľ���ʽ�����������D�����꣬��D��������������߽���ʽȷ��a��ֵ����2������û����ȷ˵�����������εĶ�Ӧ���㣬�����Ҫ��������ۣ��١�ABC�ס�BAP���ڡ�ABC�ס�PAB����3����DM��x�ύ��������M����DN��x����N����EF��DM��F���������еĶ������Q���˶�ʱ��t=BE+EFʱ��t��С���ɣ�

����Ŀ��������С�������������Խ�ߣ��¶�Խ����������С����ʾ������ı���
�������߶ȣ�ǧ�ף�h | 0 | 1 | 2 | 3 | 4 | 5 |
�¶ȣ��棩t | 20 | 14 | 8 | 2 | ��4 | ��10 |
���ݱ��У�������С���������漸�����⣬�������С���ش���������:
��1�������Ա������� ������������� �����������ϣ���h=0ʱ��ʱ���¶����� ���森
��2�������h��ʾ�������ĸ߶ȣ���t��ʾ�¶ȣ���д������t��h��ϵ��ʽ�ӣ�
��3��������������6ǧ�ĸ߿��¶��Ƕ��٣�
����Ŀ��С�ղμ�����������ɼ�ͳ�����±���
�ɼ������� |
|
|
|
|
|
���� |
|
|
|
|
|
������������ɼ�������˵����ȷ���ǣ� ��
A. ������2�� B. ��λ����8�� C. ������9�� D. ƽ������9��




