题目内容
已知在△ABC中,∠C=90°且△ABC不是等腰直角三角形,设sinB=n,当∠B是最小的内角时,n的取值范围是( )
A、0<n<
| ||||
B、0<n<
| ||||
C、0<n<
| ||||
D、0<n<
|
分析:根据三角形的内角和定理,易知直角三角形的最小内角不大于45°.
再根据sin45°=
和一个锐角的正弦值随着角的增大而增大,进行分析.
再根据sin45°=
| ||
| 2 |
解答:解:根据题意,知
0°<∠B<45°.
又sin45°=
,
∴0<n<
.
故选A.
0°<∠B<45°.
又sin45°=
| ||
| 2 |
∴0<n<
| ||
| 2 |
故选A.
点评:此题综合运用了三角形的内角和定理、特殊角的锐角三角函数值和锐角三角函数值的变化规律.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.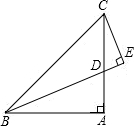 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.