Question

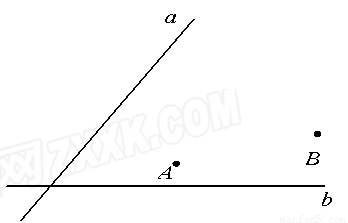
（1）数学来源于生活又服务于生活，利用数学中的几何知识可以帮助我们解决许多实际问题．李明准备与朋友合伙经营一个超市，经调查发现他家附近有两个大的居民区A、B，同时又有相交的两条公路，李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上，绘制了如图一的居民区和公路的位置图．聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置！请用尺规作图确定超市P的位置．（写出已知、求作，作图不写作法，但要求保留作图痕迹．）
（2）如图二，O为平行四边形ABCD的对角线AC的中点，过点O作一条直线分别与AB、CD交于点M、N，点E、F在直线MN上，且OE=OF．
①图中共有几对全等三角形，请把它们都写出；
②求证：∠MAE=∠NCF．

Answer 1

分析：（1）先画角的平分线，再画出线段AB的垂直平分线，两线的交点就是P．
（2）①单个三角形全等的是：△AMO≌△CNO，△AME≌△CNF．由2部分组成全等的是：△OCF≌△OAE，△ABC≌△CDA；
②由题中已知条件可证得△OCF≌△OAE，进而求得∠EAO=∠FCO，而后利用平行四边形的对边平行的性质求得相应的内错角相等，进而求解．

解答：解：（1）已知：相交直线a、b，点A、点B．
求作：点P，使点P到直线a、b的距离相等，且PA=PB．
如图所示：点P即为所求；


（2）①有4对全等三角形．
分别为△AMO≌△CNO，△OCF≌△OAE，△AME≌△CNF，△ABC≌△CDA；

②∵在△OCF与△OAE中，

OA=OC ∠1=∠2 OE=OF

，
∴△OCF≌△OAE（SAS）．
∴∠EAO=∠FCO．
在平行四边形ABCD中，AB∥CD，
∴∠BAO=∠DCO．
∴∠EAM=∠NCF．

点评：（1）考查了作图-应用与设计作图，涉及到角的平分线、线段垂直平分线的性质；
（2）找三角形全等应有规律地去找，先找单个的全等三角形，再找由2部分或2部分以上组成全等的三角形．本题的难点在于利用平行四边形的对边平行的性质得到一组内错角相等．