题目内容
 28、已知:如图,四边形ABCD是矩形(AD>AB),点E在BC上,且AE=AD,DF⊥AE,垂足为F.请探求DF与AB有何数量关系?写出你所得到的结论并给予证明.
28、已知:如图,四边形ABCD是矩形(AD>AB),点E在BC上,且AE=AD,DF⊥AE,垂足为F.请探求DF与AB有何数量关系?写出你所得到的结论并给予证明.分析:根据矩形的性质利用ASA判定△ABE≌△DFA,因为全等三角形的对应边相等,所以AB=DF.
解答:解:经探求,结论是:DF=AB.(1分)
证明:∵四边形ABCD是矩形.
∴∠B=90°,AD∥BC.
∴∠DAF=∠AEB.(2分)
∵DF⊥AE.
∴∠AFD=90°.
∵AE=AD.
∴△ABE≌△DFA.(5分)
∴AB=DF.(6分)
证明:∵四边形ABCD是矩形.
∴∠B=90°,AD∥BC.
∴∠DAF=∠AEB.(2分)
∵DF⊥AE.
∴∠AFD=90°.
∵AE=AD.
∴△ABE≌△DFA.(5分)
∴AB=DF.(6分)
点评:此题主要考查学生对矩形的性质及全等三角形的判定方法的理解及运用.

练习册系列答案
相关题目
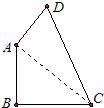 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.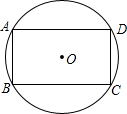 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.