Question

如图过Q点的三条直线AA′，BB′，CC′把△ABC分成六个小三角形，已知S_△AQB'=S_△BQA'=4，S_△CQA'=3，则x=S_△AQC'=________，y=S_△BQC'=________，z=S_△CQB'=________．

Answer 1

        3
分析：根据三角形的面积公式利用三角形的面积比得到x、y、z的方程组，解方程组即可．
解答：∵S_△AQB：A_△AQC=B到AA′之距：C到AA′之距=S_△BQA′：S_△CQA′，
∴（x+y）：（4+z）=4：3．
同理（4+z）：（4+3）=x：y，（4+3）：（x+y）=z：4．
三个方程相乘，得
xz=3y．
则，
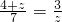解得，z=-7（舍去），z=3．
从而x=y=．
故答案为：，，3．
点评：此题考查了三角形的面积比的计算方法，能够巧妙解方程组．