题目内容
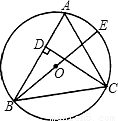
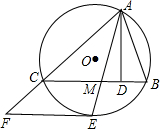△ABC的外接⊙O的半径为R，高为AD，∠BAC的平分线交⊙O于E，EF切⊙O交AC的延长线于F．结论：①AC•AB=2R•AD；②EF∥BC；③CF•AC=EF•CM；④| CM |
| BM |
| sinB |
| sinF |
| A、①②③④ | B、①②③ |
| C、②③ | D、①②④ |
分析：（1）过A作直径AN，利用直角△ACN∽直角△ADB，可得①；
（2）连接OE，由角平分线可得弧相等，即E为BC弧的中点，则OE与BC垂直，而EF是切线即EF⊥BC，得②；（3）连CE，证明△FCE∽△CMA，可得③；
（4）先把正弦化成线段的比，得到
=
，而这是角平分线定理，所以得④．
（2）连接OE，由角平分线可得弧相等，即E为BC弧的中点，则OE与BC垂直，而EF是切线即EF⊥BC，得②；（3）连CE，证明△FCE∽△CMA，可得③；
（4）先把正弦化成线段的比，得到
| CM |
| BM |
| AC |
| AB |
解答：
解：（1）过A作直径AN，连CN．则∠ACN=90°，
∵AD⊥BC，
∴∠ADB=90°，
又∵∠ANC=∠B，
∴直角△ACN∽直角△ADB，而AN=2R，
∴AC•AB=2R•AD；
（2）连接OE，
∵∠BAC的平分线交⊙O于E，
∴
=
，
∴OE⊥BC，
又∵FE是⊙O的切线，
∴FE⊥OE，
∴EF∥BC；
（3）连CE，
∵EF∥BC，
∴∠1=∠F，∠FEC=∠ECM，
又∵∠ECM=∠EAB=∠CAM，
∴△FCE∽△CMA，
∴CF•AC=EF•CM；
（4）在直角三角形ADB中，sinB=
，
在直角三角形ADC中，sin∠ACD=
，而EF∥BC，∠ACD=∠F，即sinF=
，
∴
=
，
而AM为角平分线，所以
=
，
∴
=
；
因此A对，B，C，D都错．故选A．
解：（1）过A作直径AN，连CN．则∠ACN=90°，∵AD⊥BC，
∴∠ADB=90°，
又∵∠ANC=∠B，
∴直角△ACN∽直角△ADB，而AN=2R，
∴AC•AB=2R•AD；
（2）连接OE，
∵∠BAC的平分线交⊙O于E，
∴
 |
| CE |
|
| BE |
∴OE⊥BC，
又∵FE是⊙O的切线，
∴FE⊥OE，
∴EF∥BC；
（3）连CE，
∵EF∥BC，
∴∠1=∠F，∠FEC=∠ECM，
又∵∠ECM=∠EAB=∠CAM，
∴△FCE∽△CMA，
∴CF•AC=EF•CM；
（4）在直角三角形ADB中，sinB=
| AD |
| AB |
在直角三角形ADC中，sin∠ACD=
| AD |
| AC |
| AD |
| AC |
∴
| sinB |
| sinF |
| AC |
| AB |
而AM为角平分线，所以
| AC |
| AB |
| CM |
| BM |
∴
| CM |
| BM |
| sinB |
| sinF |
因此A对，B，C，D都错．故选A．
点评：掌握使用三角形相似证明等积式或比例式．熟悉圆周角定理，角平分线定理，三角函数的定义以及切线的性质等．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
；
；
；
；
；
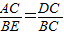
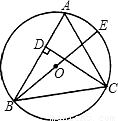
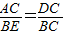
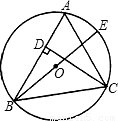
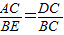
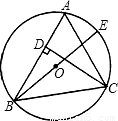