Question

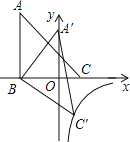
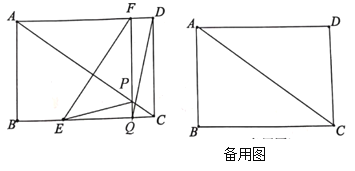
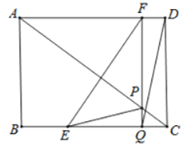
【题目】如图，在矩形中，，．如果点由点出发沿方向向点匀速运动，同时点由点出发沿方向向点匀速运动，它们的速度分别为和．过点作，分别交、于点和，设运动时间为．

（1）连结、，若四边形为平行四边形，求的值；

（2）连结，设的面积为，求与的函数关系式，并求的最大值；

（3）若与相似，求出的值．

Answer 1

【答案】（1）t＝2；（2）y有最大值，当t＝2时，y的最大值为3；（3）t的值为：2或或

【解析】

（1）通过计算发现EQ＝FQ＝6，由此即可证明．

（2）构建二次函数，利用二次函数的性质解决最值问题．

（3）分两种情形讨论，Ⅰ、如图1中，点E在Q的左侧．①当△EPQ∽△ACD时，②当△EPQ∽△CAD时，列出方程分别求解即可．Ⅱ、如图2中，点E在Q的右侧，只存在△EPQ∽△CAD列出方程即可解决．

解：（1）∵四边形ABCD是矩形，FQ⊥BC

∴∠ADC＝∠DCB＝90°，∠FQC＝90°

∴四边形CDFQ是矩形

∴FD＝QC

∴t秒后，BE＝2t，FD＝QC＝t

∴EQ＝BC﹣BE﹣QC＝8﹣3t

∵四边形EQDF为平行四边形

∴FD＝EQ 即：8﹣3t＝t

解得：t＝2

∴四边形EQDF为平行四边形时，t的值为2．

（2）∵∠FQC＝∠B＝90°

∴PQ∥AB

∴△CPQ∽△CAB

，即

∴y＝（8﹣2t）＝﹣2＋3t＝﹣（t﹣2）2＋3

∴y有最大值，当t＝2时，y的最大值为3．

（3）分两种情况讨论：

①若点E在FQ左边

当△EPQ∽△ACD时，可得，即：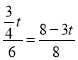

解得：t＝2

当△EPQ∽△CAD时，可得：，即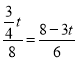

解得：

②若点E在FQ右边

当△EPQ∽△ACD时，可得：，即：

解得：t＝4（舍去）

当△EPQ∽△CAD时，可得：，即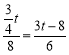

解得：

所以若△EPQ与△ADC相似，则t的值为：2或或．