题目内容
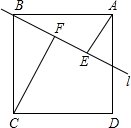如图，过正方形ABCD的顶点B作直线l，过A，C作l的垂线，垂足分别为E，F，若AE=3，CF=4，求AB的长．
解：∵∠FCB+∠CBF=90°，∠CBF+∠ABE=90°，
∴∠FCB=∠ABE，
∵过A，C作l的垂线，垂足分别为E，F，
∴∠CFB=∠AEB=90°，
∵CB=AB，
∴△CBF≌△BAE．
∴BE=CF=4，
∴AB=
=5．
所以AB的长是5．
分析：正方形的四个边都想等，四个角都是直角，根据题目所给的条件能够证明△CBF和△BAE全等，根据勾股定理可求出AB的长．
点评：本题考查正方形的性质正方形的四个角相等，四个边相等，以及全等三角形的判定和性质．
∴∠FCB=∠ABE，
∵过A，C作l的垂线，垂足分别为E，F，
∴∠CFB=∠AEB=90°，
∵CB=AB，
∴△CBF≌△BAE．
∴BE=CF=4，
∴AB=
=5．所以AB的长是5．
分析：正方形的四个边都想等，四个角都是直角，根据题目所给的条件能够证明△CBF和△BAE全等，根据勾股定理可求出AB的长．
点评：本题考查正方形的性质正方形的四个角相等，四个边相等，以及全等三角形的判定和性质．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
24、如图，在Rt△ABC与Rt△ABD中，∠ABC=∠BAD=90°，AD=BC，AC，BD相交于点G，过点A作AE∥DB交CB的延长线于点E，过点B作BF∥CA交DA的延长线于点F，AE，BF相交于点H．
17、如图，以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC，连接PE，作AD⊥BC，垂足为D，延长DA交PE于点H．过P作PM⊥DM，垂足为M，过点E作EN⊥DM，垂足为N．
