题目内容
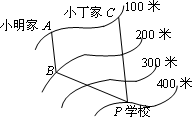
如图，∠1和∠D是直线AB、DE被直线CD
CD
所截，它们是内错角
内错角
；和∠D是同旁内角的是∠2
∠2
（只要求写一个角即可）．分析：根据同旁内角的定义，结合图形即可得出答案．
解答：解：根据图示知，∠1和∠D是直线AB、DE被直线CD所截．∠D是同旁内角的是∠2、∠E和∠DCB．
故答案可以是：∠2．
故答案可以是：∠2．
点评：本题主要考查了同旁内角的定义．三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．
练习册系列答案
相关题目
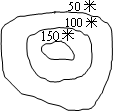
如图是9×7的正方形点阵，其水平方向和竖直方向的两格点间的长度都为1个单位，以这些点为顶点的三角形称为格点三角形．请通过画图分析、探究回答下列问题：
道BC的长86.96米，跑道的宽为l米．（π=3.14，结果精确到0.01）
＝
；
到
之间时，小明和小丁步行的平均速度均约为1.3米/秒；当坡度在
到
之间时，小明和小丁步行的平均速度均约为1米/秒)
＝
；BP的水平距离＝3.6´
50000＝180000(厘米)＝1800(米)，BP的坡度＝
＝
；CP的水平距离＝4.2´
50000＝210000(厘米)＝2100(米)，CP的坡度＝_________；
＜
＜
，所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒．因为________，所以小丁在路段CP上步行的平均速度约为________米/秒，斜坡_______AB的距离＝
»
906(米)，斜坡BP的距离＝
≈1811(米)，斜_________坡CP的距离＝
≈2121(米)，所以小明从家到学校的时间＝
________＝2090(秒)．小丁从家到学校的时间约为________秒．因此，________先到学校．