题目内容
如图,EFGH是正方形ABCD的内接四边形,两条对角线EG和FH相交于点O,且它们所夹的锐角为θ,∠BEG与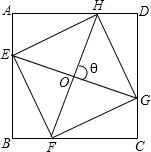 ∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,
∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,(1)求证:sinθ=
| 2S | kl |
(2)试用k、l、S来表示正方形ABCD的面积.
分析:(1)根据图形知,S=S△EFG+S△EHG=S△EOF+S△GOF+S△EOH+S△GOH,然后由面积公式S=
absinC证明结论即可;
(2)过E、F、G、H分别作AB、BC、CD、DA的垂线,构造矩形PQRT.利用勾股定理求的正方形ABCD的边长,然后由S△AEH=S△TEH,S△BEF=S△PEF,S△GFC=S△QFG,S△DGH=S△RGH推知(k2+l2-4S)a2=k2l2-4S2,最后根据(1)的结论来判定k2l2-4S2,的取值范围,从而用k、l、S来表示正方形ABCD的面积.
| 1 |
| 2 |
(2)过E、F、G、H分别作AB、BC、CD、DA的垂线,构造矩形PQRT.利用勾股定理求的正方形ABCD的边长,然后由S△AEH=S△TEH,S△BEF=S△PEF,S△GFC=S△QFG,S△DGH=S△RGH推知(k2+l2-4S)a2=k2l2-4S2,最后根据(1)的结论来判定k2l2-4S2,的取值范围,从而用k、l、S来表示正方形ABCD的面积.
解答:(1)证明:S=S△EFG+S△EHG,
=S△EOF+S△GOF+S△EOH+S△GOH,
=
EO•0F•sinθ+
GO•0F•sin(180°-θ)
+
EO•OH•sin(180°-θ)+
GO•OH•sinθ
=
EG•OF•sinθ+
EG•OH•sinθ
=
EG•FH•sinθ=
kl•sinθ
所以sinθ=
;
(2)解:过E、F、G、H分别作AB、BC、CD、DA的垂线,得矩形PQRT.
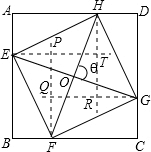 设正方形ABCD的边长为a,PQ=b,QR=c,
设正方形ABCD的边长为a,PQ=b,QR=c,
则b=
, c=
,
由S△AEH=S△TEH,
S△BEF=S△PEF,S△GFC=S△QFG,S△DGH=S△RGH
得SABCD+SPQRT=2S,
∴a2+bc=2S, 即a2+
•
=2S,
∴(k2+l2-4S)a2=k2l2-4S2,
由(1)知kl=
>2S, 所以k2+l2≥2kl>4S,
故SABCD=a2=
.
=S△EOF+S△GOF+S△EOH+S△GOH,
=
| 1 |
| 2 |
| 1 |
| 2 |
+
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
所以sinθ=
| 2S |
| kl |
(2)解:过E、F、G、H分别作AB、BC、CD、DA的垂线,得矩形PQRT.
 设正方形ABCD的边长为a,PQ=b,QR=c,
设正方形ABCD的边长为a,PQ=b,QR=c,则b=
| k2 -a2 |
| l2 -a2 |
由S△AEH=S△TEH,
S△BEF=S△PEF,S△GFC=S△QFG,S△DGH=S△RGH
得SABCD+SPQRT=2S,
∴a2+bc=2S, 即a2+
| k2-a2 |
| l2-a2 |
∴(k2+l2-4S)a2=k2l2-4S2,
由(1)知kl=
| 2S |
| sinθ |
故SABCD=a2=
| k2l2-4S2 |
| k2+l2-4S |
点评:本题主要考查了三角形的面积、正方形的性质及正、余弦定理.此题难度较大,在解题时需灵活运用正、余弦定理.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
