题目内容
 如图,⊙O与⊙M相交于A,B,半径是2,⊙O过点M,则S四边形OAMB=________.
如图,⊙O与⊙M相交于A,B,半径是2,⊙O过点M,则S四边形OAMB=________.
2
分析:根据相交两圆的性质得出四边形AOBM是菱形,进而得出AB,OM的长,即可得出答案.
解答: 解:连接AB,OM,
解:连接AB,OM,
由题意可得出:AO=MO=AM=OB=BM=2,
AB⊥MO,
∴四边形AOBM是菱形,
∴AN= =
= ,则AB=2
,则AB=2 ,
,
∴S四边形OAMB= AB×MO=
AB×MO= ×2
×2 ×2=2
×2=2 .
.
故答案为:2 .
.
点评:此题主要考查了相交两圆的性质以及菱形的判定与性质,根据已知得出AB的长是解题关键.

分析:根据相交两圆的性质得出四边形AOBM是菱形,进而得出AB,OM的长,即可得出答案.
解答:
 解:连接AB,OM,
解:连接AB,OM,由题意可得出:AO=MO=AM=OB=BM=2,
AB⊥MO,
∴四边形AOBM是菱形,
∴AN=
 =
= ,则AB=2
,则AB=2 ,
,∴S四边形OAMB=
 AB×MO=
AB×MO= ×2
×2 ×2=2
×2=2 .
.故答案为:2
 .
.点评:此题主要考查了相交两圆的性质以及菱形的判定与性质,根据已知得出AB的长是解题关键.

练习册系列答案
相关题目
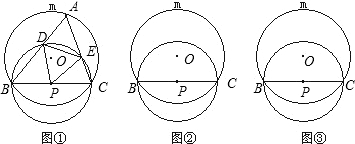
 延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F.
延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F.


 如图,⊙O与⊙O′相交,AB为公共弦,圆心距⊙OO′=5cm,⊙O与⊙O′的半径分别为4cm和3cm,则AB的长为
如图,⊙O与⊙O′相交,AB为公共弦,圆心距⊙OO′=5cm,⊙O与⊙O′的半径分别为4cm和3cm,则AB的长为 如图,⊙O与⊙M相交于A,B,半径是2,⊙O过点M,则S四边形OAMB=
如图,⊙O与⊙M相交于A,B,半径是2,⊙O过点M,则S四边形OAMB=