题目内容
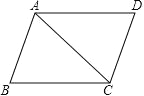
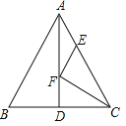
【题目】如图在![]() 中,
中,![]() 是
是![]() 的中线,
的中线,![]() 是
是![]() 上的动点,
上的动点,![]() 是边
是边![]() 上动点,则
上动点,则![]() 的最小值为______________.
的最小值为______________.
【答案】![]()
【解析】
作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,根据等腰三角形“三线合一”得出BD的长和AD⊥BC,再利用勾股定理求出AD,利用“等面积法”结合垂线段最短进一步求出最小值即可.
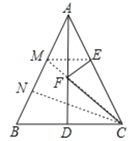
如图,作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是△ABC的中线,
∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,
在Rt△ABD中,由勾股定理可得:
AD=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵E关于AD的对称点M,
∴EF=FM,
∴CF+EF=CF+FM=CM,
根据垂线段最短可得:CM≥CN,
即:CF+EF≥![]() ,
,
∴CF+EF的最小值为:![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目