Question

观察，探究下面用绳子捆扎半径都为3圆柱管的截面图（圆柱管是单层水平放置）．
根据上述图示，写出以下问题中的绳子长（接头不计）：
（1）捆扎2个圆柱管的绳子长为______；
（2）捆扎n个圆柱管的绳子长为______（用含n代数式表示）．

Answer 1

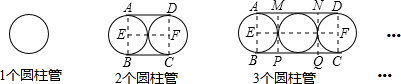
解：（1）∵==3π，AD=BC=6，
捆扎2个圆柱管的绳子长为++AD+BC=12+6π；
（2）捆扎2个圆柱管的绳子长=12+6π=12×1+6π；
∵==3π，AD=BC=AM+MN+ND=3+6+3=12，
捆扎3个圆柱管的绳子长为++AD+BC=24+6π=12×2+6π，
…，
依据此规律，归纳得：
捆扎n个圆柱管的绳子长为12（n-1）+6π．
故答案为：12+6π；12（n-1）+6π
分析：（1）由两圆相切时，圆心距等于两半径相加，求出EF的长，即为AD与BC的长，再由两半圆AB与CD的弧长之和为一个圆的周长，根据圆的半径求出一个圆的周长，由圆周长+AD+BC即可表示出捆扎2个圆柱管的绳子长；
（2）由（1）表示出的捆扎2个圆柱管的绳子长；以及如图所示，第三个图形中根据AM+MN+ND求出AD的长，即为BC的长，再由圆周长+AD+BC即可表示出捆扎3个圆柱管的绳子长，…，依此类推，可推出捆扎n个圆柱管的绳子长．
点评：此题考查了两圆相切的性质，以及圆周长的计算方法，锻炼了学生归纳总结的能力，是中考中常考的热点试题．