题目内容
△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD=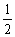 BC.动点M从点C出发,以每秒1个单
BC.动点M从点C出发,以每秒1个单 位的速度沿CA向点A
位的速度沿CA向点A 运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
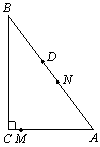

⑴ 求cosA的值.
⑵ 当以MN为直径的圆与△ABC一边相切时,求t的值.
解:⑴ 设BC=4m,AC=x,则BD=2m,AD=x
-- ∵ 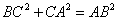 ∴ 16
∴ 16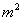 +
+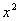 =
=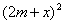
-- 解之得 x=3m
-- 从而AB=5m
-- 因此cosA=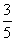
⑵ CM=t,AM=7-t,DN=2t,AN=7-2t,其中0≤t≤3.5
-- 记以MN为直径的圆为⊙O,当⊙O与AB相切时,则MN⊥AB,
因此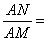
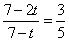 ,t=2,符合题意;
,t=2,符合题意;
-- 当⊙O与AC相切时,则MN⊥AC,因此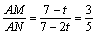 ,t=-14,舍去;6分
,t=-14,舍去;6分
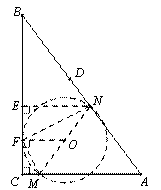 -- 当⊙O与BC相切时,
-- 当⊙O与BC相切时,
-- 如图,作NE⊥BC,垂足为E.取EC的中点F,连结OF,则OF⊥BC,即点F为⊙O与BC相切的切点.连结MF,NF,则FM⊥FN,因此△FCM∽△NEF.
-- 因此CM·EN=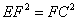
-- 而CM= t,EN=
t,EN=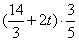 ,
,
EF=FC=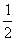 EC=
EC=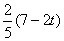
-- 因此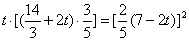 ,整理得
,整理得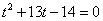
-- 解之得 t=1,t=-14(舍去) --------------------------------- 综上所得,当以MN为直径的圆与△ABC一边相切时,t=1或t=2. ---------------------------------- 10分

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
| 选 手 | 甲 | 乙 | 丙 | 丁 |
| 平均数(环) | 9.2 | 9.2 |
| 9.2 |
| 方差(环2) | 0.035 | 0.015 | 0.025 | 0.027 |
则这四人中成绩发挥最稳定的是
A.甲 B.乙 C.丙 D.丁
 ,其中a=
,其中a= ,b=
,b=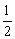 .
.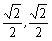 ),将线段OP0绕点O按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1绕点O按
),将线段OP0绕点O按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1绕点O按 逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2014的坐标是
逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2014的坐标是 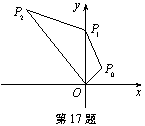


 ,那么
,那么 =_________
=_________