题目内容
如图,△AOB和△BCD都是等边三角形,点A、C在函数 的图象上,并且边OB、BD都在x轴正半轴上,若OA=4,则点C的横坐标为 .
的图象上,并且边OB、BD都在x轴正半轴上,若OA=4,则点C的横坐标为 .
【答案】分析:作AE⊥x轴于E,CF⊥x轴于F,利用特殊角的三角函数值反比例函数的解析式即可求出A点的坐标,BC=a,根据特殊角的三角函数值及等边三角形的性质即可求出BF的长,进一步求出C点坐标即可.
解答: 解:作AE⊥x轴于E,CF⊥x轴于F.
解:作AE⊥x轴于E,CF⊥x轴于F.
于是EA=OA•sin60°=4sin60°=4× =2
=2 ,
,
OE=4cos60°=4× =2,A点坐标为(2,2
=2,A点坐标为(2,2 ),
),
代入解析式y= 得,k=4
得,k=4 ,解析式为y=
,解析式为y= ;
;
设BC=a,则BF= a,CF=asin60°=
a,CF=asin60°= a,
a,
C点坐标为(4+ a,
a, a),d代入解析式y=
a),d代入解析式y= 得
得
(4+ a)×
a)× a=4
a=4 ,a=4+4
,a=4+4 或a=-4
或a=-4 -4(负值舍去),BF=-2+2
-4(负值舍去),BF=-2+2 .
.
∴点C的横坐标为4+(-2+2 )=2+2
)=2+2 .
.
故答案为:2+2 .
.
点评:解答此题要充分利用等边三角形的性质,用一边长表示出各线段的长,将A、C点坐标用含a的代数式表示出来,代入反比例函数解析式求值即可解答.
解答:
 解:作AE⊥x轴于E,CF⊥x轴于F.
解:作AE⊥x轴于E,CF⊥x轴于F.于是EA=OA•sin60°=4sin60°=4×
 =2
=2 ,
,OE=4cos60°=4×
 =2,A点坐标为(2,2
=2,A点坐标为(2,2 ),
),代入解析式y=
 得,k=4
得,k=4 ,解析式为y=
,解析式为y= ;
;设BC=a,则BF=
 a,CF=asin60°=
a,CF=asin60°= a,
a,C点坐标为(4+
 a,
a, a),d代入解析式y=
a),d代入解析式y= 得
得(4+
 a)×
a)× a=4
a=4 ,a=4+4
,a=4+4 或a=-4
或a=-4 -4(负值舍去),BF=-2+2
-4(负值舍去),BF=-2+2 .
.∴点C的横坐标为4+(-2+2
 )=2+2
)=2+2 .
.故答案为:2+2
 .
.点评:解答此题要充分利用等边三角形的性质,用一边长表示出各线段的长,将A、C点坐标用含a的代数式表示出来,代入反比例函数解析式求值即可解答.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 15、如图,∠AOB和一条定长线段a,在∠AOB内找一点P,使P到OA,OB的距离都等于a,做法如下:
15、如图,∠AOB和一条定长线段a,在∠AOB内找一点P,使P到OA,OB的距离都等于a,做法如下: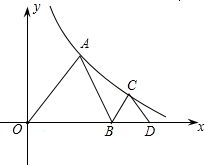 如图,△AOB和△BCD都是等边三角形,点A、C在函数
如图,△AOB和△BCD都是等边三角形,点A、C在函数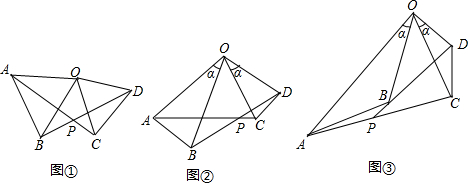
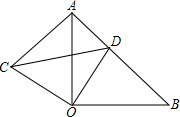 如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.
如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上. 如图,∠AOB和∠AOD分别是∠AOC的余角和补角,且OC是∠BOD的平分线,求∠AOC的度数.
如图,∠AOB和∠AOD分别是∠AOC的余角和补角,且OC是∠BOD的平分线,求∠AOC的度数.