题目内容
如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
A. | B. | C. | D. |
B
解析试题分析:连接OC,则∠DCO=∠BCO,∠FCO=∠ECO,
∴∠DCO-∠FCO=∠BCO-∠ECO,即∠DCF=∠BCE,
又∵△BCE沿着CE折叠至△FCE,
∴∠BCE=∠ECF,
∴∠BCE=∠ECF=∠BCE=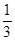 ∠BCD=30°,
∠BCD=30°,
∴∠CEB=60°
在RT△BCE中,设BE=x,则CE=2x,
得CE2=BC2+BE2,即4x2=x2+42,
解得x= ,
,
∴CE=2x= .
.
故选B.
考点:翻折变换(折叠问题).
点评:解答本题的关键是根据切线的性质得到∠BCE=∠ECF=∠BCE=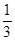 ∠BCD=30°,有一定难度.
∠BCD=30°,有一定难度.

练习册系列答案
相关题目
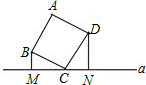 如图正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长为( )
如图正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长为( )| A、1 | ||
| B、2 | ||
| C、4 | ||
D、
|
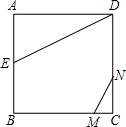 如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似?
如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似? 如图正方形ABCD的边BC的延长线上取点M,使CM=AC=2,AM与CD相交于点N,∠ANC=
如图正方形ABCD的边BC的延长线上取点M,使CM=AC=2,AM与CD相交于点N,∠ANC= (2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点. 如图正方形ABCD的边长是a,△AEF是等边三角形,点E在BC上,点F在CD上
如图正方形ABCD的边长是a,△AEF是等边三角形,点E在BC上,点F在CD上