Question

【题目】如图所示，在△ABC中，，BP，BQ三等分，CP，CQ三等分，求的度数.

Answer 1

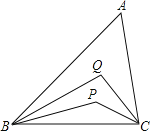
【答案】∠BPC=140°.

【解析】

由∠A=60°，根据三角形的内角和定理得，∠ABC+∠ACB=180°-60°=120°，再由线段BP、BQ把∠ABC三等分，线段CP、CQ把∠ACB三等分，得到∠PBC=

∠ABC，∠PCB=∠ACB，于是∠PBC+∠PCB=（∠ABC+∠ACB）=×120°=40°，再根据三角形的内角和定理得，∠BPC=180°-40°=140°

∵∠A=60°

∴∠ABC+∠ACB=180°-60°=120°

又∵∠PBC=∠ABC

又∵线段CP，CQ三等分∠ACB

∴∠PCB=∠ACB

∴∠PBC+∠PCB=(∠ABC+∠ACB)=×120°=40°

∴∠BPC=180°-40°=140°.