题目内容
已知:矩形ABCD中,AB=6,∠BAC=30o,点E在CD上,
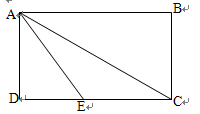
小题1:若AE=4,求:梯形AECB的面积;
小题2:若点F在AC上,且∠AFB=∠CEA,求: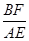 的值。
的值。

小题1:若AE=4,求:梯形AECB的面积;
小题2:若点F在AC上,且∠AFB=∠CEA,求:
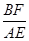 的值。
的值。小题1:(1).10
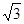
小题2:(2).
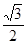
分析:(1)在△ABC中,利用∠BAC=30°的正切求出BC的长,再根据勾股定理,利用△ADE的三边求出DE的长度,即可求出EC,代入梯形面积公式即可求解.
(2)求出对角线AC的值,利用△ABF和△CAE相似的性质即可求解.
解:∵矩形ABCD,
∴∠ABC=∠D=90°,AD=BC,CD=AB=6,(1分)
在Rt△ABC中,AB=6,∠BAC=30°,BC=ABtan∠BAC=2
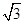 ,(2分)
,(2分)(1)在Rt△ADE中,AE=4,AD=BC=2
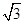 ,
,∴DE=
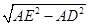 =2
=2∴EC=6-2=4.
∴梯形ABCE的面积S=
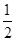 (EC+AB)?BC=
(EC+AB)?BC=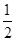 (4+6)×2
(4+6)×2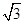 =10
=10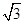 .(3分)
.(3分)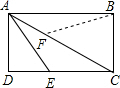
(2)在Rt△ABC中,AB=6,∠BAC=30°,
∴AC=AB÷cos30°=4
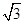 ,
,在矩形ABCD中,AB∥CD,
∴∠BAC=∠ACD,
∵∠BFA=∠CEA,
∴△ABF∽△CAE,
∴
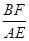 =
=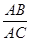 =
=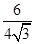 =
= .
.
练习册系列答案
相关题目
 的两条对角线相交于点
的两条对角线相交于点 ,
, ,则矩形的对角线
,则矩形的对角线 的长是( )
的长是( )



 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.

 的最小值是
的最小值是 ,则AB长为
,则AB长为