题目内容
两个相似多边形的面积之比为1:3,则它们周长之比为
- A.1:3
- B.1:9
- C.1:

- D.2:3
C
分析:由于面积之比等于相似比的平方,所以周长之比等于相似比,就可求解.
解答:根据题意得:周长之比为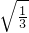 =1:
=1: .
.
故选C
点评:本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.
分析:由于面积之比等于相似比的平方,所以周长之比等于相似比,就可求解.
解答:根据题意得:周长之比为
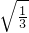 =1:
=1: .
.故选C
点评:本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.

练习册系列答案
相关题目
如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为( )
| A、9:4 | B、2:3 | C、3:2 | D、81:16 |
两个相似多边形的面积比是9:16,其中小多边形的周长为36cm,则较大多边形的周长为( )
| A、48cm | B、54cm | C、56cm | D、64cm |