题目内容
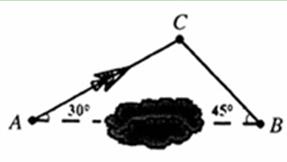
如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的方向成30°角的方向飞行,飞行到中途,再沿与原来的飞行方向成45°角的方向继续飞行直到到终点.这样飞机的飞行路程比原来的路程600km远了 多少?(参考数据:
多少?(参考数据:| 3 |
| 2 |
分析:过点C作CD⊥AB于点D,由锐角三角函数的定义可得出AD=
,BD=
,由AD+BD=AB可求出CD的值,再分别在Rt△ACD、Rt△BCD中利用勾股定理即可求出AC、BC的长,进而可得出结论.
| CD |
| tan30° |
| CD |
| tan45° |
解答: 解:过点C作CD⊥AB于点D,则AD=
解:过点C作CD⊥AB于点D,则AD=
,BD=
,
∵AD+BD=AB,
∴(
+1)CD=600,
∴CD=300(
-1),
∴在Rt△ACD中,AC=600(
-1),在Rt△BCD中,BC=300
(
-1),
AC+BC=600(
-1)+300
(
-1)≈746.79(km),
747-600=147(km),
答:飞机的飞行路程比原来的路程600km远了147km.
 解:过点C作CD⊥AB于点D,则AD=
解:过点C作CD⊥AB于点D,则AD=| CD |
| tan30° |
| CD |
| tan45° |
∵AD+BD=AB,
∴(
| 3 |
∴CD=300(
| 3 |
∴在Rt△ACD中,AC=600(
| 3 |
| 2 |
| 3 |
AC+BC=600(
| 3 |
| 2 |
| 3 |
747-600=147(km),
答:飞机的飞行路程比原来的路程600km远了147km.
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

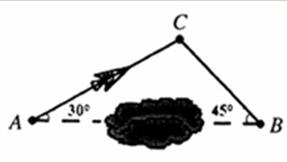
 角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终
角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终 点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
 ≈1.73,
≈1.73, ≈1.41.要求在结果化简后再代入参考数据运算,结果保留整数)
≈1.41.要求在结果化简后再代入参考数据运算,结果保留整数)
 ≈1.73,
≈1.73, ≈1.41.要求在结果化简后再代入参考数据运算,结果保留整数)
≈1.41.要求在结果化简后再代入参考数据运算,结果保留整数)