题目内容
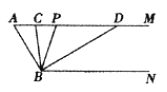
【题目】如图,直线AB与CD相较于点O,OE⊥AB与点O,OB平分∠DOF,∠DOE=62°.
求∠AOC、∠EOF、∠COF的度数。

【答案】∠AOC =28°,∠EOF=118°,∠COF=124°
【解析】
根据OE⊥AB,得出∠BOE=90°,再由∠DOE=62°,得出∠BOD,由对顶角相等得出∠AOC的度数,根据角平分线的定义求出∠DOF,由∠DOF+∠DOE得出∠EOF的度数,最后由∠DOC是平角得出∠COF的度数即可.
∵OE⊥AB,
∴∠BOE=90°,
∵∠DOE=62°,
∴∠BOD=90°-62°=28°,
∴∠AOC=∠BOD=28°,
∵OB平分∠DOF,
∴∠DOF=2∠BOD=2×28°=56°,
∴∠EOF=∠DOF+∠DOE=118°
又∵点O在CD上,
∴∠COF=180°-∠DOF=180°-56°=124°.
即:∠AOC =28°,∠EOF=118°,∠COF=124°

练习册系列答案
相关题目