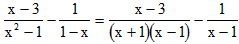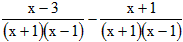题目内容
先化简,再求值: ,其中x=1+tan60°.
,其中x=1+tan60°.
解:原式= •
•
= ,
,
当x=1+tan60°=1+ 时,原式=
时,原式= =
= .
.
分析:利用完全平方公式和平方差公式,括号里面的式子的分子分母分别分解因式,然后利用除以一个数等于乘以这个数的倒数把除法运算化为乘法运算,约分后得到最简结果,然后利用特殊角的三角函数值确定出x的值,把x的值代入化简的式子中即可求出值.
点评:此题考查了分式的化简求值,分式的乘除关键是约分,约分的关键是找出公因式,若出现分子或分母中出现多项式,应先将多项式进行因式分解再约分.本题属于化简求值题,解答此类题要先将原式化为最简,再代值,同时本题注意特殊角的三角函数值的应用.
 •
•
=
 ,
,当x=1+tan60°=1+
 时,原式=
时,原式= =
= .
.分析:利用完全平方公式和平方差公式,括号里面的式子的分子分母分别分解因式,然后利用除以一个数等于乘以这个数的倒数把除法运算化为乘法运算,约分后得到最简结果,然后利用特殊角的三角函数值确定出x的值,把x的值代入化简的式子中即可求出值.
点评:此题考查了分式的化简求值,分式的乘除关键是约分,约分的关键是找出公因式,若出现分子或分母中出现多项式,应先将多项式进行因式分解再约分.本题属于化简求值题,解答此类题要先将原式化为最简,再代值,同时本题注意特殊角的三角函数值的应用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
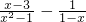 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: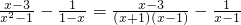
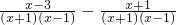
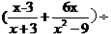
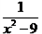 ,其中
,其中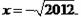 小张同学做题时把“
小张同学做题时把“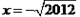 ”错写成了“
”错写成了“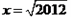 ”,但他的计算结果也是正确的,请你解释这是怎么回事?
”,但他的计算结果也是正确的,请你解释这是怎么回事?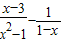 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: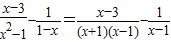
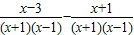
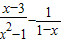 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: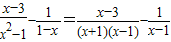
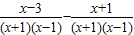
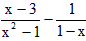 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: