题目内容
 如图所示的抛物线是
如图所示的抛物线是 的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.
的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.
(1)当∠APB=90°时,求点P的坐标及抛物线的解析式;
(2)求上述抛物线所对应的二次函数在0<x≤7时的最大值和最小值.
 解:(1)过P作PC⊥AB于C,设平移后抛物线的解析式为y=-
解:(1)过P作PC⊥AB于C,设平移后抛物线的解析式为y=- (x-h)2+t,
(x-h)2+t,则P点坐标为(h,t).
在直角三角形PAC中,∠PAB=45°,
因此PC=AC,即t=h-1.
由于抛物线过A点,则有:

解得:
 ,
, (不合题意舍去)
(不合题意舍去)因此抛物线的解析式为y=-
 (x-3)2+2.
(x-3)2+2.(2)根据(1)的二次函数关系式可知:
当x=3时,ymax=2
当x=7时,ymin=-6.
分析:(1)可设平移后的抛物线的解析式为y=-
 (x-h)2+t,那么抛物线的顶点P为(h,t).由于△AMP是等腰直角三角形,如果过P作x轴的垂线不难得出t=h-1,那么抛物线的解析式可写成:y=-
(x-h)2+t,那么抛物线的顶点P为(h,t).由于△AMP是等腰直角三角形,如果过P作x轴的垂线不难得出t=h-1,那么抛物线的解析式可写成:y=- (x-h)2+h-1,将A点坐标代入抛物线的解析式中即可得出h和t的值,进而可求出P点坐标和抛物线的解析式.
(x-h)2+h-1,将A点坐标代入抛物线的解析式中即可得出h和t的值,进而可求出P点坐标和抛物线的解析式.(2)可根据(1)的二次函数解析式和自变量的取值范围求出函数的最大和最小值.
点评:本题主要考查了二次函数的平移以及函数解析式的确定及性质等知识点.弄清二次函数图象平移前后解析式的区别是解题的关键.

练习册系列答案
相关题目
 的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.
的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.
 的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.
的图象经平移而得到的,此时抛物线过点A(1,0)和x轴上点A右侧的点B,顶点为P.
 的图象的一段,斜坡的截线OA在
的图象的一段,斜坡的截线OA在 一次函数
一次函数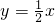 的图象的一段,建立如图所示的直角坐标系.
的图象的一段,建立如图所示的直角坐标系. 的图象的一段,斜坡的截线OA在一次函数
的图象的一段,斜坡的截线OA在一次函数 的图象的一段,建立如图所示的直角坐标系.
的图象的一段,建立如图所示的直角坐标系.