Question

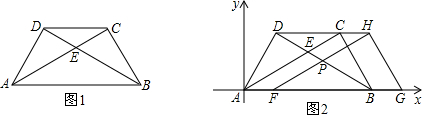
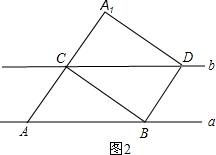
如图1，若四边形ABCD、四边形CFED都是正方形，显然图中有AG=CE，AG⊥CE.
【小题1】当正方形GFED绕D旋转到如图2的位置时，AG=CE， AG⊥CH是否成立？若成立，请给出证明；若不成立，请说明理由.
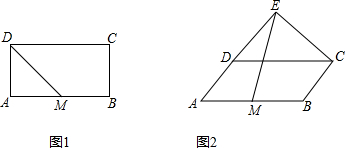
【小题2】当正方形GFED绕D旋转到如图3的位置时，延长CE交AG于H，交AD于M.当AD=4，DG=时，求CH的长。

Answer 1

【小题1】AG=CE， AG⊥CH成立
【小题2】CH=解析:
解：（1）成立．
四边形、四边形是正方形，
∴    ……………1分
∠∠.
∴∠90°-∠∠.                          ……………2分
∴△△.
∴.               ……………3分
（1）可得△△，
∴∠1＝∠2              …………………4分
又∵∠＝∠. 
∴∠∠＝.
即            …………………5分
（1）解法一: 过作于,
（2）
由题意有,
∴，则∠1＝.   ………6分
而∠1＝∠2，∴∠2＝＝∠1＝.
∴　，即.         …………………7分
在Rt中，＝＝,………8分
而∽,∴,　 即,　　　　
∴.　                                …………………9分
再连接，显然有,
∴.
所求的长为.                            …………………10分
解法二：研究四边形ACDG的面积
过作于,

由题意有,
∴,.        ………………8分
而以CD为底边的三角形CDG的高=PD=1,
,
∴4×1+4×4=×CH+4 ×1.
∴=.               ………………10分