题目内容
已知：如图，以线段AB为直径作半圆O1，以线段AO1为直径作半圆O2，半径O1C交半圆O2于D点．试比较 |
| AC |
|
| AD |
分析：连接O2D，根据⊙O1的半径是⊙O2的直径，确定其为O1A：O2A=2：1，根据圆周角与圆心角的关系，∠1=2∠2，利用扇形弧长公式即可求出两个扇形的弧长，比较即可．
解答：
解：如图：连接O2D，
∵O1A：O2A=2：1，
∴设O1A=2x，O2A=x；
根据同弧所对的圆周角是圆心角的一半，∠1=2∠2，
设∠2=y度，则∠1=2y度，
=
=
；
=
=
；
可见，
与
的长度相等．
解：如图：连接O2D，∵O1A：O2A=2：1，
∴设O1A=2x，O2A=x；
根据同弧所对的圆周角是圆心角的一半，∠1=2∠2，
设∠2=y度，则∠1=2y度，
|
| AC |
| yπ2x |
| 180 |
| πxy |
| 90 |
|
| AD |
| 2yπx |
| 180 |
| πxy |
| 90 |
可见，
|
| AC |
|
| AD |
点评：本题考查了弧长的计算，同时涉及到圆周角与圆心角的关系，解题中要注意设出相关量进行计算．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
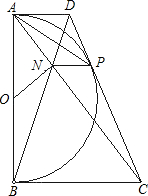已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A、B），过点P作半圆O的切线分别交过A、B两点的切线于D、C，AC、BD相交于N点，连接ON、NP．下列结论：①四边形ANPD是梯形；②ON=NP；③PA为∠NPD的平分线．其中一定成立的是（ ）
交过A、B两点的切线于D、C，连接OC、BP，过点O作OM∥CD分别交BC与BP于点M、N．下列结论：
已知：如图，以线段AB为直径作半圆O1，以线段AO1为直径作半圆O2，半径O1C交半圆O2于D点．试比较
与
的长．
与
的长．