题目内容
如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.
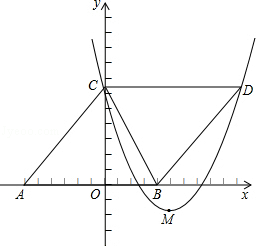
(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.

(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
解:(1)证明:∵A(﹣6,0),B(4,0),C(0,8),
∴AB=6+4=10, 。∴AB=AC。
。∴AB=AC。
由翻折可得,AB=BD,AC=CD。∴AB=BD=CD=AC。∴四边形ABCD是菱形。
∴CD∥AB。
∵C(0,8),∴点D的坐标是(10,8)。
(2)∵y=ax2﹣10ax+c,∴对称轴为直线 。
。
设M的坐标为(5,n),直线BC的解析式为y=kx+b,
∴ ,解得
,解得 。
。
∴直线BC的解析式为y=﹣2x+8。
∵点M在直线y=﹣2x+8上,∴n=﹣2×5+8=﹣2。
∴M(5,,-2).
又∵抛物线y=ax2﹣10ax+c经过点C和M,
∴ ,解得
,解得 。
。
∴抛物线的函数表达式为 。
。
(3)存在。点P的坐标为P1( ),P2(﹣5,38)
),P2(﹣5,38)
∴AB=6+4=10,
 。∴AB=AC。
。∴AB=AC。由翻折可得,AB=BD,AC=CD。∴AB=BD=CD=AC。∴四边形ABCD是菱形。
∴CD∥AB。
∵C(0,8),∴点D的坐标是(10,8)。
(2)∵y=ax2﹣10ax+c,∴对称轴为直线
 。
。设M的坐标为(5,n),直线BC的解析式为y=kx+b,
∴
 ,解得
,解得 。
。∴直线BC的解析式为y=﹣2x+8。
∵点M在直线y=﹣2x+8上,∴n=﹣2×5+8=﹣2。
∴M(5,,-2).
又∵抛物线y=ax2﹣10ax+c经过点C和M,
∴
 ,解得
,解得 。
。∴抛物线的函数表达式为
 。
。(3)存在。点P的坐标为P1(
 ),P2(﹣5,38)
),P2(﹣5,38)试题分析:(1)根据勾股定理,翻折的性质可得AB=BD=CD=AC,根据菱形的判定和性质可得点D的坐标。
(2)根据对称轴公式可得抛物线的对称轴,设M的坐标为(5,n),直线BC的解析式为y=kx+b,根据待定系数法可求M的坐标,再根据待定系数法求出抛物线的函数表达式。
(3)分点P在CD的上面下方和点P在CD的上方两种情况,根据等底等高的三角形面积相等可求点P的坐标:
设P
 ,
,当点P在CD的上面下方,根据菱形的性质,知点P是AD与抛物线
 的交点,由A,D的坐标可由待定系数法求出AD的函数表达式:
的交点,由A,D的坐标可由待定系数法求出AD的函数表达式:  ,二者联立可得P1(
,二者联立可得P1( );
);当点P在CD的上面上方,易知点P是∠D的外角平分线与抛物线
 的交点,此时,∠D的外角平分线与直线AD垂直,由相似可知∠D的外角平分线PD的斜率等于-2,可设其为
的交点,此时,∠D的外角平分线与直线AD垂直,由相似可知∠D的外角平分线PD的斜率等于-2,可设其为 ,将D(10,8)代入可得PD的函数表达式:
,将D(10,8)代入可得PD的函数表达式:  ,与抛物线
,与抛物线 联立可得P2(﹣5,38)。
联立可得P2(﹣5,38)。
练习册系列答案
相关题目
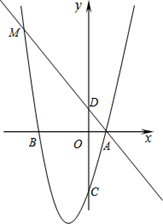
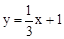 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.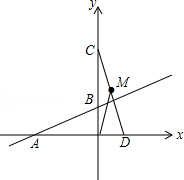
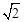 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.
 与x轴相交于O、B,顶点为A,连接OA.
与x轴相交于O、B,顶点为A,连接OA.

 .
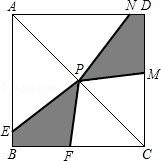
. 、二次函数
、二次函数 和反比例函数
和反比例函数 在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】
在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】