题目内容
 (2012•东莞模拟)如图,九年级某班同学要测量校园内旗杆的高度,在地面的C点处用测角器测得旗杆顶A点的仰角∠AFE=45°,再沿直线CB后退12m到D点,在D点又用测角器测得旗杆顶A点的仰角∠AGE=30°;已知测角器的高度为1.7m,求旗杆AB的高度(结果保留一位小数).
(2012•东莞模拟)如图,九年级某班同学要测量校园内旗杆的高度,在地面的C点处用测角器测得旗杆顶A点的仰角∠AFE=45°,再沿直线CB后退12m到D点,在D点又用测角器测得旗杆顶A点的仰角∠AGE=30°;已知测角器的高度为1.7m,求旗杆AB的高度(结果保留一位小数).分析:由∠AFE=45°,得到△AEF为等腰Rt△,AE=EF,在Rt△AEG中,GE=
AE,根据GE-EF=GF=12,计算出AE,然后由AB=AE+EF,得到AB.
| 3 |
解答:解:∵∠AFE=45°,
∴△AEF为等腰Rt△,
∴AE=EF
∵∠AGE=30°,
在Rt△AEG中,GE=
AE,
又∵GE-EF=GF=12,即有(
-1)AE=12,
∴AE=16.38米,
∴AB=AE+BE=16.38+1.7=17.98≈18.1米.
答:求旗杆高度约为18.1米.
∴△AEF为等腰Rt△,
∴AE=EF
∵∠AGE=30°,
在Rt△AEG中,GE=
| 3 |
又∵GE-EF=GF=12,即有(
| 3 |
∴AE=16.38米,
∴AB=AE+BE=16.38+1.7=17.98≈18.1米.
答:求旗杆高度约为18.1米.
点评:本题考查了仰角的应用;也考查了把实际问题转化为数学问题的能力以及含30度的直角三角形三边的关系.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
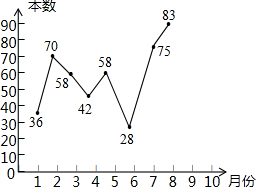 (2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
(2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )