题目内容
方程ax2+bx+c=0，当c= 时，方程有一根为0；若有一根为1，则a+b+c= ；
若方程有且只有一根为0，则a= ，c= ．
【答案】分析：方程有一根是0，代入方程即可得到c=0，当c=0时，方程是ax2+bx=0，一定有一根是0；
将x=1代入即可求出a+b+c的值；
若方程有且只有一根为0，则方程一定是一元一次方程，a=0，b≠0，且c=0．
解答：解：（1）方程有一根为0
把x=0代入方程ax2+bx+c=0可得：c=0；
（2）当有一根为1时，ax2+bx+c=0变为a+b+c=0；
∴a+b+c=0；
（3）当方程有且只有一根为0时，
方程是一元一次方程，则a=0，c=0．
点评：一元二次方程若有解则方程一定有两个解，方程的两个解相同时不能认为是只有一个解．
将x=1代入即可求出a+b+c的值；
若方程有且只有一根为0，则方程一定是一元一次方程，a=0，b≠0，且c=0．
解答：解：（1）方程有一根为0
把x=0代入方程ax2+bx+c=0可得：c=0；
（2）当有一根为1时，ax2+bx+c=0变为a+b+c=0；
∴a+b+c=0；
（3）当方程有且只有一根为0时，
方程是一元一次方程，则a=0，c=0．
点评：一元二次方程若有解则方程一定有两个解，方程的两个解相同时不能认为是只有一个解．
练习册系列答案
阅读快车系列答案
相关题目
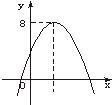9、已知抛物线y=ax2+bx+c如图所示，则关于x的方程ax2+bx+c-8=0的根的情况是（ ）
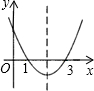己知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：（1）4a+2b+c＜0；（2）方程ax2+bx+c=0两根都大于零；（3）y随x的增大而增大；（4）一次函数y=x+bc的图象一定不过第二象限．其中正确的个数是（ ）
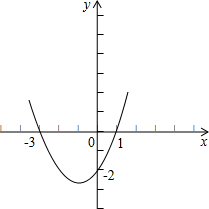已知函数y=ax2+bx+c的图象如图所示，试根据图象回答下列问题：