题目内容
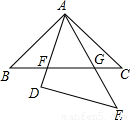
如图,△ABC与△DEA是两个全等的等腰三角形,∠BAC=∠D=90°,BC分别与AD、AE相交于点F、G,BF≠CG.(1)图中有那几对不全等的相似三角形,请把他们表示出来.
(2)根据甲、乙两位同学对图形的探索,试探究BF、FG、GC之间的关系,并证明.
甲同学:把△ABF、△AGC分别沿AD、AE折叠,发现:B、C两点重合.
乙同学:把△ABF绕点A旋转,使AB、AC重合,发现:构造出了直角.
【答案】分析:(1)直接根据相似三角形判定定理找出所有不全等的相似三角形的个数;
(2)方法(一)把△ABF、△AGC分别沿AD、AE折叠,利用三角形全等的知识证明∠FPG=∠B+∠C=90°,进而可以证明BF、FG、GC之间的关系;
方法(二)标出∠1、∠2、∠3、∠4,把△ABF旋转至△ACP,得△ABF≌△ACP,再利用三角形全等的知识证明∠ACP+∠ACB=90°,进而可以证明BF、FG、GC之间的关系;
解答:解:(1)共有3对,
△GAF∽△GAB;
△FAC∽△FGA;
△ABG∽△FAC;
(2)证明方法(一)
如图1,把△ABF、△AGC分别沿AD、AE折叠,
得△ABF≌△APF,△ACG≌△APG,B、C两点重合,
BF=FP,CG=GP,
∠FPG=∠B+∠C=90°,
在RT△PFG中,GF2=BF2+GC2;
证明方法(二)把△ABF旋转至△ACP,得△ABF≌△ACP,
∠1=∠4,AF=AP,CP=BF,∠ACP=∠B,
∠1+∠3=45°,
∠4+∠3=45°,
∠2=∠4+∠3=45°,
AG=AG,
△AFG≌△AGP,FG=GP,
∠ACP+∠ACB=90°,
在RT△PGG中,GF2=CG2+CP2,
GF2=BF2+GC2.
点评:本题主要考查几何变换综合题,解答本题的关键是熟练掌握旋转知识,全等三角形的证明,此类题也是中考经常涉及的考题类型,此题难度不大.
(2)方法(一)把△ABF、△AGC分别沿AD、AE折叠,利用三角形全等的知识证明∠FPG=∠B+∠C=90°,进而可以证明BF、FG、GC之间的关系;
方法(二)标出∠1、∠2、∠3、∠4,把△ABF旋转至△ACP,得△ABF≌△ACP,再利用三角形全等的知识证明∠ACP+∠ACB=90°,进而可以证明BF、FG、GC之间的关系;
解答:解:(1)共有3对,
△GAF∽△GAB;
△FAC∽△FGA;
△ABG∽△FAC;
(2)证明方法(一)

如图1,把△ABF、△AGC分别沿AD、AE折叠,
得△ABF≌△APF,△ACG≌△APG,B、C两点重合,
BF=FP,CG=GP,
∠FPG=∠B+∠C=90°,
在RT△PFG中,GF2=BF2+GC2;
证明方法(二)把△ABF旋转至△ACP,得△ABF≌△ACP,

∠1=∠4,AF=AP,CP=BF,∠ACP=∠B,
∠1+∠3=45°,
∠4+∠3=45°,
∠2=∠4+∠3=45°,
AG=AG,
△AFG≌△AGP,FG=GP,
∠ACP+∠ACB=90°,
在RT△PGG中,GF2=CG2+CP2,
GF2=BF2+GC2.
点评:本题主要考查几何变换综合题,解答本题的关键是熟练掌握旋转知识,全等三角形的证明,此类题也是中考经常涉及的考题类型,此题难度不大.

练习册系列答案
相关题目
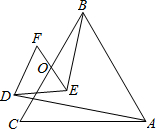 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )A、
| ||
B、
| ||
| C、5:3 | ||
| D、不确定 |
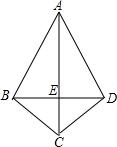 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.
22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.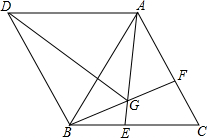 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G. 29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.
29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.