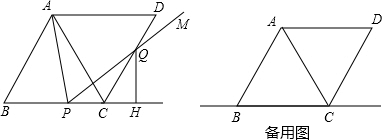
题目内容
菱形ABCD中,∠B=60°,延长BC到E,使得CE=BC,连接DE.
(1)如图1,M是BC的中点,线段AM和ME之间的数量关系为
(2)如图2,P是直线AB上的任意一点,M是CP的中点,过点M作MF⊥AM交DE于点F,探究线段AM与MF之间的数量关系,并证明你的结论.

(1)如图1,M是BC的中点,线段AM和ME之间的数量关系为
AM=
ME
| ||
| 3 |
AM=
ME
.
| ||
| 3 |
(2)如图2,P是直线AB上的任意一点,M是CP的中点,过点M作MF⊥AM交DE于点F,探究线段AM与MF之间的数量关系,并证明你的结论.

分析:(1)如图1,连接AC.先证明△ABC是等边三角形,得出AB=BC=AC,再根据等腰三角形三线合一的性质得出AM⊥BC,然后在Rt△ABM中,由正弦函数的定义得出AM=
AB,又AB=
ME,代入得出AM=
ME;
(2)如图2,延长AM、DC,交于点Q,连接AC,在DE上截取DF′=CQ,连接AF′、QF′,先利用SAS证明△ADF′≌△ACQ,得出AF′=AQ,∠DAF′=∠CAQ,进而得到△AF′Q是等边三角形,再利用AAS证明△PAM≌△CQM,再证明△AQF是等边三角形,然后在Rt△AMF中,由正切函数的定义得出AM=
ME.
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
(2)如图2,延长AM、DC,交于点Q,连接AC,在DE上截取DF′=CQ,连接AF′、QF′,先利用SAS证明△ADF′≌△ACQ,得出AF′=AQ,∠DAF′=∠CAQ,进而得到△AF′Q是等边三角形,再利用AAS证明△PAM≌△CQM,再证明△AQF是等边三角形,然后在Rt△AMF中,由正切函数的定义得出AM=
| ||
| 3 |
解答: 解:(1)如图1,连接AC.
解:(1)如图1,连接AC.
∵菱形ABCD中,∠B=60°,
∴△ABC是等边三角形,AB=BC=AC,
∵M是BC的中点,
∴AM⊥BC,
∴AM=ABsin∠B=
AB.
∵ME=MC+CE=
BC+BC=
BC=
AB,
∴AB=
ME,
∴AM=
×
ME=
ME,即AM=
ME;
(2)如图2,延长AM、DC,交于点Q,连接AC,在DE上截取DF′=CQ,连接AF′、QF′.
∵CE=BC=CD,∠DCE=∠B=60°,
∴△CDE是等边三角形,
∴∠E=60°.
在△ADF′与△ACQ中,
,
∴△ADF′≌△ACQ,
∴AF′=AQ,∠DAF′=∠CAQ.
∵∠F′AQ=∠F′AC+∠CAQ=∠F′AC+∠DAF′=∠DAC=60°,
∴△AF′Q是等边三角形.
∵AB∥DQ,
∴∠PAM=∠CQM,∠APM=∠QCM.
在△PAM与△CQM中,
,
∴△PAM≌△CQM,
∴AM=QM,
∵AF′=QF′,
∴MF′⊥AM,
∵MF⊥AM,
∴F与F′重合,
∴△AQF是等边三角形,
∴
=tan∠AFM=tan30°=
,
∴AM=
MF.
故答案为AM=
ME.
 解:(1)如图1,连接AC.
解:(1)如图1,连接AC.∵菱形ABCD中,∠B=60°,
∴△ABC是等边三角形,AB=BC=AC,
∵M是BC的中点,
∴AM⊥BC,
∴AM=ABsin∠B=
| ||
| 2 |
∵ME=MC+CE=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴AB=
| 2 |
| 3 |
∴AM=
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
| ||
| 3 |
(2)如图2,延长AM、DC,交于点Q,连接AC,在DE上截取DF′=CQ,连接AF′、QF′.
∵CE=BC=CD,∠DCE=∠B=60°,
∴△CDE是等边三角形,
∴∠E=60°.
在△ADF′与△ACQ中,
|
∴△ADF′≌△ACQ,
∴AF′=AQ,∠DAF′=∠CAQ.
∵∠F′AQ=∠F′AC+∠CAQ=∠F′AC+∠DAF′=∠DAC=60°,
∴△AF′Q是等边三角形.
∵AB∥DQ,
∴∠PAM=∠CQM,∠APM=∠QCM.
在△PAM与△CQM中,
|
∴△PAM≌△CQM,
∴AM=QM,
∵AF′=QF′,
∴MF′⊥AM,
∵MF⊥AM,
∴F与F′重合,
∴△AQF是等边三角形,
∴
| AM |
| MF |
| ||
| 3 |
∴AM=
| ||
| 3 |
故答案为AM=
| ||
| 3 |
点评:此题主要考查了菱形的性质,等边三角形、相似三角形、全等三角形的判定与性质,锐角三角函数的定义,垂线的性质,综合性较强,有一定难度.(2)中准确作出辅助线,证明出△AQF是等边三角形是解题的关键.

练习册系列答案
相关题目
 5、如图,在菱形ABCD中,点E,F分别是AB,AC的中点,如果EF=3,那么菱形ABCD的周长是( )
5、如图,在菱形ABCD中,点E,F分别是AB,AC的中点,如果EF=3,那么菱形ABCD的周长是( ) 23、如图,在菱形ABCD中,∠ADB与∠ABD的大小关系是( )
23、如图,在菱形ABCD中,∠ADB与∠ABD的大小关系是( ) 18、已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.
18、已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.