题目内容
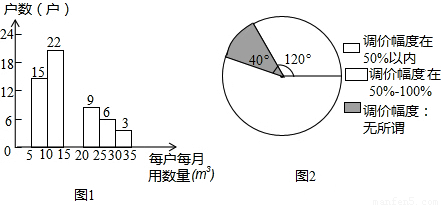
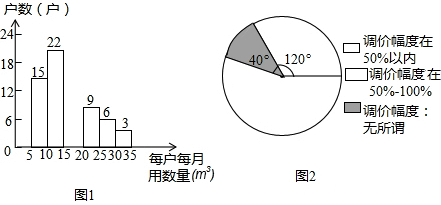
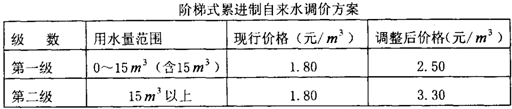
B市为制定居民用水价格调整方案,就每月的用水量、可承受的水价调整幅度等进行民意调查,调查采用随机抽样的方式.图1、图2为某一小区的调查数据统计图.已知被调查居民用户每月的用水量在5m3~35m3之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
(1)图1使用的统计图表的名称是______,它是表示一组数据______的量(填“平均水平”、“离散程度”或“分布情况”);
(2)上述两个统计图表是否完整,若不完整,试把它们补全;
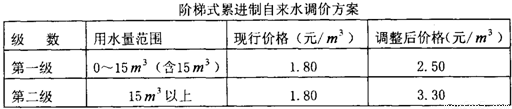
(3)若采用阶梯式累进制调价方案(如表1所示),试估计该小区有百分之几的居民用水费用的增长幅度不超过50%?
解:(1)频数分布直方图,分布情况;
(2)∵40°÷360°= ,
,
∴8÷ =72,
=72,
∴72-(15+22+9+6+3)=17.
统计图表如下所示:

(3)设每月每户用水量为xm3的居民调价后用水费用的增长幅度不超过50%,
当x≤15时,水费的增长幅度为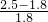 ×100%<50%;
×100%<50%;
当x>15时,则15×2.5+3.3(x-15)≤1.5×1.8x,
解得x≤20,
∵从调查数据看,每月的用水量不超过20m3的居民有15+22+17=54户,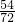 =75%,
=75%,
又∵调查是随机抽样,
∴该小区有75%的居民用水费用的增长幅度不超过50%.
故答案为:频数分布直方图,分布情况.
分析:(1)根据条形图中,各长方形之间有空隙,而直方图中,各长方形是靠在一起的,中间无空隙,可知图1使用的统计图表是频数分布直方图,它能清楚地显示各组频数的分布情况;
(2)先根据被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,中心角为40°,占 ,可求出此次抽查的总人数,再根据各小组频数之和等于总人数求出居民用户每月的用水量在15m3~20m3之间的户数;
,可求出此次抽查的总人数,再根据各小组频数之和等于总人数求出居民用户每月的用水量在15m3~20m3之间的户数;
(3)设每月每户用水量为xm3的居民调价后用水费用的增长幅度不超过50%,分情况讨论:
当x≤15时,水费的增长幅度为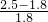 ×100%<50%;
×100%<50%;
当x>15时,利用15×2.5+3.3(x-15)≤1.5×1.8x,即可求出相应x的值,进而可求出,样本中每月的用水量不超过20m3的居民有15+22+17=54户,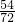 =75%,利用样本估计总体即可.
=75%,利用样本估计总体即可.
点评:本题考查的是频数分布直方图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.频数分布直方图能清楚地显示各组频数的分布情况;扇形统计图直接反映部分占总体的百分比大小.
(2)∵40°÷360°=
 ,
,∴8÷
 =72,
=72,∴72-(15+22+9+6+3)=17.
统计图表如下所示:

(3)设每月每户用水量为xm3的居民调价后用水费用的增长幅度不超过50%,
当x≤15时,水费的增长幅度为
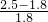 ×100%<50%;
×100%<50%;当x>15时,则15×2.5+3.3(x-15)≤1.5×1.8x,
解得x≤20,
∵从调查数据看,每月的用水量不超过20m3的居民有15+22+17=54户,
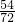 =75%,
=75%,又∵调查是随机抽样,
∴该小区有75%的居民用水费用的增长幅度不超过50%.
故答案为:频数分布直方图,分布情况.
分析:(1)根据条形图中,各长方形之间有空隙,而直方图中,各长方形是靠在一起的,中间无空隙,可知图1使用的统计图表是频数分布直方图,它能清楚地显示各组频数的分布情况;
(2)先根据被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,中心角为40°,占
 ,可求出此次抽查的总人数,再根据各小组频数之和等于总人数求出居民用户每月的用水量在15m3~20m3之间的户数;
,可求出此次抽查的总人数,再根据各小组频数之和等于总人数求出居民用户每月的用水量在15m3~20m3之间的户数;(3)设每月每户用水量为xm3的居民调价后用水费用的增长幅度不超过50%,分情况讨论:
当x≤15时,水费的增长幅度为
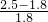 ×100%<50%;
×100%<50%;当x>15时,利用15×2.5+3.3(x-15)≤1.5×1.8x,即可求出相应x的值,进而可求出,样本中每月的用水量不超过20m3的居民有15+22+17=54户,
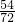 =75%,利用样本估计总体即可.
=75%,利用样本估计总体即可.点评:本题考查的是频数分布直方图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.频数分布直方图能清楚地显示各组频数的分布情况;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 个水龙头、
个水龙头、 个抽水马桶漏水.若一万个漏水的水龙头一个月能漏掉a立方米水;一万个漏水的马桶一个月漏掉b立方米水,则全市一个月仅这两项所造成的水流失量是多少?
个抽水马桶漏水.若一万个漏水的水龙头一个月能漏掉a立方米水;一万个漏水的马桶一个月漏掉b立方米水,则全市一个月仅这两项所造成的水流失量是多少?