Question

【题目】边长为1的正方形OABC的顶点A在X轴的正半轴上，如图将正方形OABC绕顶点O顺时针旋转75°得正方形OABC，使点B恰好落在函数y=ax2（a<0）的图像上，

则a的值为___________.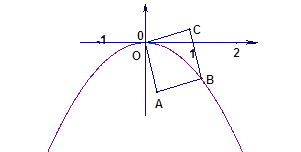

Answer 1

【答案】

【解析】

此题考查图形旋转问题，求出B点坐标代入函数就可以了．

解：连接OB，

∵旋转75°，

∴x轴正半轴与OA的夹角为75°，

∵∠AOB=45°，

∴OB与x轴正半轴夹角为75°-45°=30°，

过B作BD⊥x轴于D，

∵BC=OC=1，∴OB=，

∴BD=，

∴OD=，

∴B（，-），

把B点坐标代入y=ax2中得：-=()2a，

解之得：a=-．

题主要考查坐标转换问题，先给一个确定的坐标再通过旋转求出旋转以后的坐标，问题就解决了．