题目内容
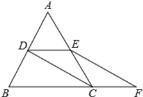
【题目】如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )

A. 点G B. 点E C. 点D D. 点F
【答案】A
【解析】如下图,过点D作DM⊥OB于点M,则∠OME=90°,
∵在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,
∴点A的坐标为(9,12),点B的坐标为(18,0),点C的坐标为(18,12),∠OBC=90°=∠ACB,△ACD∽△BDO,△OMD∽△OBC,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴DM=8,OM=12,
∴点D的坐标为(12,8),
∵点点E、F、G分别是CD、BD、BC的中点,
∴点E、F、G的坐标分别为(15,10)、(15,4)、(18,6),
∵在点A(9,12)中,9×12=108;点E(15,10)中,15×10=150;点F(15,4)中,15×4=60;点G(18,6)中18×6=1-8;
∴点A和点G中同一反比例函数的图象上.
故选A.


【题目】2019年4月29日至2019年10月7日,2019年中国北京世界园艺博览会(简称北京世园会)在中国北京市延庆区举行,展期162天.这是继云南昆明后第二个获得国际园艺生产者协会批准及国际展览局认证授权举办的A1级国际园艺博览会.北京世园会门票种类分为平日票、指定日票、三次票等票种,同时按销售对象分为普通票、优惠票和团队票(学生享受优惠票,15人以上可以享受团体票).指定日包括开园日、“五一”假期、端午节假期、中秋节假期、“十一”假期这些日期,其余时间为平日;三次票是指除指定日外,同一持票人在展会期间可以任选三天入园的票种. 具体如下表:
平日票价(元/张) | 指定日票价(元/张) | 三次票(元/张) | |
普通票 | 120 | 160 | 300 |
优惠票 | 80 | 100 |
小明,小亮两家共10人打算一起参观北京世园会(10人均需购票).
(1)若他们端午节去北京世园会参观购买门票共用去1360元,问买了普通票和优惠票各几张?
(2)如果他们平日去北京世园会参观,且购买门票的费用不超过2000元,那么在保证游玩的前提下最多可以买几张三次票?共有几种买票方案?分别是什么?