题目内容
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
【答案】
(1)解:已知:抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣9;
x﹣9;
当x=0时,y=﹣9,则:C(0,﹣9);
当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣9=0,得:x1=﹣3,x2=6,则:A(﹣3,0)、B(6,0);
x﹣9=0,得:x1=﹣3,x2=6,则:A(﹣3,0)、B(6,0);
∴AB=9,OC=9
(2)解:∵ED∥BC,
∴△AED∽△ABC,
∴ ![]() =(
=( ![]() )2,即:
)2,即: ![]() =(
=( ![]() )2,得:s=
)2,得:s= ![]() m2(0<m<9)
m2(0<m<9)
(3)解:解法一:∵S△ACE= ![]() AEOC=
AEOC= ![]() m×9=
m×9= ![]() m,
m,
∴S△CDE=S△ACE﹣S△ADE= ![]() m﹣
m﹣ ![]() m2=﹣
m2=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() .
.
∵0<m<9,
∴当m= ![]() 时,S△CDE取得最大值,最大值为
时,S△CDE取得最大值,最大值为 ![]() .此时,BE=AB﹣AE=9﹣
.此时,BE=AB﹣AE=9﹣ ![]() =
= ![]() .
.
记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC= ![]() =
= ![]() =3
=3 ![]() .
.
∵∠OBC=∠MBE,∠COB=∠EMB=90°.
∴△BO∽△BME,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴r= ![]() =
= ![]() .
.
∴所求⊙E的面积为:π( ![]() )2=
)2= ![]() π.
π.
解法二:∵S△AEC= ![]() AEOC=
AEOC= ![]() m×9=
m×9= ![]() m,
m,
∴S△CDE=S△AEC﹣S△ADE= ![]() m﹣
m﹣ ![]() m2=﹣
m2=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() .
.
∵0<m<9,
∴当m= ![]() 时,S△CDE取得最大值,最大值为
时,S△CDE取得最大值,最大值为 ![]() .此时,BE=AB﹣AE=9﹣
.此时,BE=AB﹣AE=9﹣ ![]() =
= ![]() .
.
∴S△EBC= ![]() S△ABC=
S△ABC= ![]() .
.
如图2,记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC= ![]() =
= ![]() .
.
∵S△EBC= ![]() BCEM,∴
BCEM,∴ ![]() ×
× ![]() r=
r= ![]() ,
,
∴r= ![]() =
= ![]() .
.
∴所求⊙E的面积为:π( ![]() )2=
)2= ![]() π.
π.
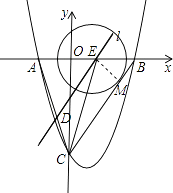
【解析】(1)已知抛物线的解析式,当x=0,可确定C点坐标;当y=0时,可确定A、B点的坐标,进而确定AB、OC的长.(2)直线l∥BC,可得出△AED、△ABC相似,它们的面积比等于相似比的平方,由此得到关于s、m的函数关系式;根据题干条件:点E与点A、B不重合,可确定m的取值范围.(3)①首先用m列出△AEC的面积表达式,△AEC、△AED的面积差即为△CDE的面积,由此可得关于S△CDE、m的函数关系式,根据函数的性质可得到S△CDE的最大面积以及此时m的值;②过E做BC的垂线EM,这个垂线段的长即为与BC相切的⊙E的半径,可根据相似三角形△BEF、△BCO得到的相关比例线段求得该半径的值,由此得解.

【题目】为了支持国货,哈市某手机卖场计划用![]() 万元购进华为品牌手机.从卖场获知华为品牌
万元购进华为品牌手机.从卖场获知华为品牌![]() 种不同型号的手机的进价及售价如下表:
种不同型号的手机的进价及售价如下表:
|
|
| |
进价(元/部) |
|
|
|
售价(元/部) |
|
|
|
若该手机卖场同时购进两种不同型号的手机![]() 台,
台,![]() 万元刚好用完.
万元刚好用完.
(1)请您确定该手机的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售的利润![]() 的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?