题目内容

已知点P（a，b）是双曲线y=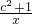 $数学公式$ （c为常数）和直线y=- $数学公式$ x+1的一个交点，则a²+b²+c²的值是________．

$\text{[math]}$
分析：将P（a，b）分别代入两解析式，根据纵坐标相等，建立等式，找到a、c之间的关系式，利用非负数的性质解答即可．
解答：将P（a，b）分别代入两解析式得，b= 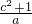$\text{[math]}$ ，b=- $\text{[math]}$ a+1；
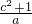于是 $\text{[math]}$ =- $\text{[math]}$ a+1；
整理得，4c²+（a-2）²=0；
根据非负数的性质，c=0，a=2．
见a=2代入y=- $\text{[math]}$ x+1得，y=- $\text{[math]}$ ×2+1= $\text{[math]}$ ，
即b= $\text{[math]}$ ．
于是a²+b²+c²=2²+（ $\text{[math]}$ ）²+0²= $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：此题综合性较强，不仅考查两个函数交点的坐标满足这两个函数关系式，还考查了非负数的性质．在解题时要注意，先将数值代入，然后根据式子特点，找到合适的方法（利用非负数的性质）解答．