题目内容
两个同心圆的半径分别为3 cm和4 cm,大圆的弦BC与小圆相切,则BC=________cm.
2
分析:设两个同心圆的圆心为O,连接OB,O与BC的切点,在构建的直角三角形中,由勾股定理即可求得BC的长.
解答: 解:如图;设BC与小圆的切点为D;连接OB、OD;
解:如图;设BC与小圆的切点为D;连接OB、OD;
∵BC与小圆相切,
∴∠ODB=90°;
在Rt△OBD中,OB=4cm,OD=3cm,
由勾股定理,得:BD= =
= cm;
cm;
∴BC=2BD=2 cm.
cm.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

分析:设两个同心圆的圆心为O,连接OB,O与BC的切点,在构建的直角三角形中,由勾股定理即可求得BC的长.
解答:
 解:如图;设BC与小圆的切点为D;连接OB、OD;
解:如图;设BC与小圆的切点为D;连接OB、OD;∵BC与小圆相切,
∴∠ODB=90°;
在Rt△OBD中,OB=4cm,OD=3cm,
由勾股定理,得:BD=
 =
= cm;
cm;∴BC=2BD=2
 cm.
cm.点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
两个同心圆的半径分别为1cm和2cm,大圆的弦AB与小圆相切,那么AB=( )
| A、1cm | ||
B、2
| ||
| C、3cm | ||
| D、4cm |
 8、如图,两个同心圆的半径分别为5和3,将半径为3的小圆沿直线m水平向右平移2个单位,则平移后的小圆与大圆的位置关系是( )
8、如图,两个同心圆的半径分别为5和3,将半径为3的小圆沿直线m水平向右平移2个单位,则平移后的小圆与大圆的位置关系是( )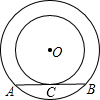 如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB=( )
如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB=( )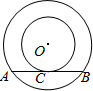 如图,两个同心圆的半径分别为6cm和10cm,弦AB与小圆相切于点C,则AB=
如图,两个同心圆的半径分别为6cm和10cm,弦AB与小圆相切于点C,则AB=