题目内容
8．在平面直角坐标系内有四个点A（-3，-2），B（-3，9），C（-5.1），D（7，1），连接AB和CD，则线段AB和CD的位置关系是垂直．分析 根据A、B的横坐标相同，得到AB∥y轴，由C、D的纵坐标相同，所以CD∥x轴，即可得到AB⊥CD．
解答 解：∵A、B的横坐标相同，
∴AB∥y轴，
∵C、D的纵坐标相同，
∴CD∥x轴，
∵x轴⊥y轴，
∴AB⊥CD．
故答案为：垂直．
点评 本题考查了坐标与图形的性质，解决本题的关键是熟记点的横坐标相同，与y轴平行，点的纵坐标相同，与x轴平行．
练习册系列答案
相关题目
18．若关于x的方程（2m+3）x=n-2有无数解，则m，n需要满足的条件是（ ）
| A． | m≠-$\frac{3}{2}$，n≠2 | B． | m≠-$\frac{3}{2}$，n=2 | C． | m=-$\frac{3}{2}$，n≠2 | D． | m=-$\frac{3}{2}$，n=2 |
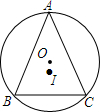如图，△ABC中，AB=AC=13，BC=10，⊙O为△ABC外接圆，I为△ABC的内心．
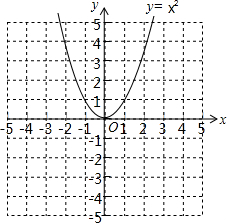二次函数y=x2的图象如图，请将此图象向右平移1个单位，再向下平移4个单位．
