题目内容
如图,已知直线![]() 过点
过点![]() 和
和![]() ,
,![]() 是
是![]() 轴正半轴上的动点,
轴正半轴上的动点,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)直接写出直线![]() 的解析式;
的解析式;
(2)设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于t的函数关系式;并求出当
关于t的函数关系式;并求出当![]() 时,
时,![]() 的最大值;
的最大值;
(3)直线![]() 过点
过点![]() 且与
且与![]() 轴平行,问在
轴平行,问在![]() 上是否存在点
上是否存在点![]() , 使得
, 使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
 |
(1)![]()
(2)∵![]() ,∴
,∴![]() 点的横坐标为
点的横坐标为![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,
,
∴![]() .
.
②当![]() 时,
时,![]() ,
,
∴![]() .
.
∴
当![]() ,即
,即![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
(3)由![]() ,所以
,所以![]() 是等腰直角三角形,若在
是等腰直角三角形,若在![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则![]() ,所以
,所以![]() ,又
,又![]() 轴,则
轴,则![]() ,
,![]() 两点关于直线
两点关于直线![]() 对称,所以
对称,所以![]() ,得
,得![]() .
.
下证![]() .连
.连![]() ,则四边形
,则四边形![]() 是正方形.
是正方形.
法一:(i)当点![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上
上
(![]() 与
与![]() 不重合)时,如图1.
不重合)时,如图1.
 |
由对称性,得![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
(ii)当点![]() 在线段
在线段![]() 的延长线上,
的延长线上,![]() 在线段
在线段![]() 上时,如图2,如图3
上时,如图2,如图3
∵![]() , ∴
, ∴![]() .
.
(iii)当点![]() 与点
与点![]() 重合时,显然
重合时,显然![]() .
.
综合(i)(ii)(iii),![]() .
.
 ∴在
∴在![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形.
为直角顶点的等腰直角三角形.
 |
法二:由![]() ,所以
,所以![]() 是等腰直角三角形,若在
是等腰直角三角形,若在![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则![]() ,所以
,所以![]() ,又
,又![]() 轴, 则
轴, 则![]() ,
,![]() 两点关于直线
两点关于直线![]() 对称,所以
对称,所以![]() ,得
,得![]() .
.
延长![]() 与
与![]() 交于点
交于点![]() .
.
(i)如图4,当点![]() 在线段
在线段![]() 上(
上(![]() 与
与![]() 不重合)时,
不重合)时,
∵四边形![]() 是正方形,
是正方形,
∴四边形![]() 和四边形
和四边形![]() 都是矩形,
都是矩形,![]() 和
和![]() 都是等腰直角三角形.
都是等腰直角三角形.
∴![]() .
.
又∵![]() , ∴
, ∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
(ii)当点![]() 与点
与点![]() 重合时,显然
重合时,显然![]() .
.
(iii)![]() 在线段
在线段![]() 的延长线上时,如图5,
的延长线上时,如图5,
∵![]() ,∠1=∠2
,∠1=∠2
∴![]()
综合(i)(ii)(iii),![]() .
.
∴在![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形.
为直角顶点的等腰直角三角形.
 | |||
 | |||
法三:由![]() ,所以
,所以![]() 是等腰直角三角形,若在
是等腰直角三角形,若在![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则![]() ,所以
,所以![]() ,又
,又![]() 轴,
轴,
则![]() ,O两点关于直线
,O两点关于直线![]() 对称,所以
对称,所以![]() ,得
,得![]() .
.
连![]() ,∵
,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
∴![]() ,∴
,∴![]() .
.
∴在![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形.
为直角顶点的等腰直角三角形.

 )作x轴的平行线分别交双曲线y=
)作x轴的平行线分别交双曲线y=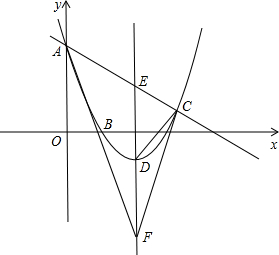 如图,已知抛物线过点A(0,6),B(2,0),C(7,
如图,已知抛物线过点A(0,6),B(2,0),C(7, (2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=
(2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=