题目内容
根据下列表格对应值：
判断关于x的方程ax2+bx+c=0（a≠0）的一个解x的范围是（ ）
| x | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.02 | 0.01 | 0.03 |
| A、x＜3.24 |
| B、3.24＜x＜3.25 |
| C、3.25＜x＜3.26 |
| D、3.25＜x＜3.28 |
考点：估算一元二次方程的近似解
专题：
分析：观察表格可知，随x的值逐渐增大，ax2+bx+c的值在3.24～3.25之间由负到正，故可判断ax2+bx+c=0时，对应的x的值在3.24＜x＜3.25之间．
解答：解：由图表可知，ax2+bx+c=0时，3.24＜x＜3.25．
故选B．
故选B．
点评：本题考查了估算一元二次方程的近似解，关键是观察表格，确定函数值由负到正（或由正到负）时，对应的自变量取值范围．
练习册系列答案
阅读快车系列答案
相关题目
作图题（保留作图痕迹，不写作法）．
如图，以矩形ABDE的一边BD为直径作半圆O，BE交圆O于C，AC的延长线交ED于M，交BD的延长线于N，若ME=MC．
如图，在平面直角坐标系中，反比例函数y1=
矩形ABCD的长AD=a，宽AB=b，E、F分别是AD、BC 上的点，BE、DF是相距为h的平行线，求AE的长（用a、b、h表示）．
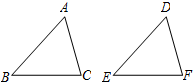如图，给出下列四组条件，其中，不能使△ABC≌△DEF的条件是（ ）| A、AB=DE，BC=EF，AC=DF |
| B、AB=DE，∠B=∠E，BC=EF |
| C、∠B=∠E，BC=EF，∠C=∠F |
| D、AB=DE，AC=DF，∠B=∠E |